Minimal surfaces from circle patterns: Geometry from
... should understand its Gauss map and the combinatorics of the curvature line pattern. The image of the curvature line pattern under the Gauss map provides us with a cell decomposition of (a part of) S 2 or a covering. From these data, applying the Koebe theorem, we obtain a circle packing with the pr ...
... should understand its Gauss map and the combinatorics of the curvature line pattern. The image of the curvature line pattern under the Gauss map provides us with a cell decomposition of (a part of) S 2 or a covering. From these data, applying the Koebe theorem, we obtain a circle packing with the pr ...
Projective limits of topological vector spaces
... clean presentation of projective and direct limits, and also Paul Garrett’s notes Functions on circles and Basic categorical constructions, which are on his homepage. I have not used them, but J. L. Taylor, Notes on locally convex topological vector spaces looks readable and comprehensive. ...
... clean presentation of projective and direct limits, and also Paul Garrett’s notes Functions on circles and Basic categorical constructions, which are on his homepage. I have not used them, but J. L. Taylor, Notes on locally convex topological vector spaces looks readable and comprehensive. ...
Convex Sets and Convex Functions on Complete Manifolds
... The aim of this paper is to show how convex sets and functions give strong restrictions to the topology of a certain class of complete Riemannian manifolds without boundary. The idea of convexity plays an essential role for the proofs of "finiteness theorems", which give a priori estimates for the n ...
... The aim of this paper is to show how convex sets and functions give strong restrictions to the topology of a certain class of complete Riemannian manifolds without boundary. The idea of convexity plays an essential role for the proofs of "finiteness theorems", which give a priori estimates for the n ...
Course 212: Academic Year 1991-2 Section 4: Compact Topological
... Proof Let V be a collection of open sets in Y which covers f (A). Then A is covered by the collection of all open sets of the form f −1 (V ) for some V ∈ V. It follows from the compactness of A that there exists a finite collection V1 , V2 , . . . , Vk of open sets belonging to V such that A ⊂ f −1 ...
... Proof Let V be a collection of open sets in Y which covers f (A). Then A is covered by the collection of all open sets of the form f −1 (V ) for some V ∈ V. It follows from the compactness of A that there exists a finite collection V1 , V2 , . . . , Vk of open sets belonging to V such that A ⊂ f −1 ...
4 COMPACTNESS AXIOMS
... of subsets of X is said to have the finite intersection property (fip) iff every finite subfamily has a non-empty intersection. Now suppose that X is a topological space. An open cover of A is a cover consisting of open subsets of X. Local and point finiteness of covers are obvious extensions of Def ...
... of subsets of X is said to have the finite intersection property (fip) iff every finite subfamily has a non-empty intersection. Now suppose that X is a topological space. An open cover of A is a cover consisting of open subsets of X. Local and point finiteness of covers are obvious extensions of Def ...
Order, topology, and preference
... This is part of ongoing research on 'planning and control for multiple objectives' being conducted within the MIPC (Management Information for Planning and Control) Group at The author wishes the Sloan School of Management, M.I.T. to acknowledge a helpful discussion with Paul Kleindorfer. ...
... This is part of ongoing research on 'planning and control for multiple objectives' being conducted within the MIPC (Management Information for Planning and Control) Group at The author wishes the Sloan School of Management, M.I.T. to acknowledge a helpful discussion with Paul Kleindorfer. ...
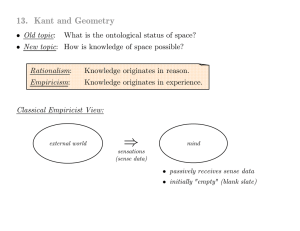
13.Kant and Geometry
... "The apodeictic certainty of all geometrical propositions, and the possibility of their a priori construction, is grounded in this a priori necessity of space. Were this representation of space a concept acquired a posteriori, and derived from outer experience in general, the first principles of mat ...
... "The apodeictic certainty of all geometrical propositions, and the possibility of their a priori construction, is grounded in this a priori necessity of space. Were this representation of space a concept acquired a posteriori, and derived from outer experience in general, the first principles of mat ...
Hyperbolic Geometry and 3-Manifold Topology
... so that for each component T of ∂M , the inclusion C ∩ T → T is a homotopy equivalence. Such a C is called a relative core. Relative cores are not needed for this paper. They play an important role in the parabolic case. Definition 1.12. An end E of a manifold M is an equivalence class of nested seq ...
... so that for each component T of ∂M , the inclusion C ∩ T → T is a homotopy equivalence. Such a C is called a relative core. Relative cores are not needed for this paper. They play an important role in the parabolic case. Definition 1.12. An end E of a manifold M is an equivalence class of nested seq ...
Math 3329-Uniform Geometries — Lecture 13 1. A model for
... points. The lines in spherical geometry are the great circles. Great circles are those circles on the sphere that have the same radius as the sphere (in this case r = 1). They also divide the sphere exactly in half. The equator is a great circle, and any circle passing through both the north pole an ...
... points. The lines in spherical geometry are the great circles. Great circles are those circles on the sphere that have the same radius as the sphere (in this case r = 1). They also divide the sphere exactly in half. The equator is a great circle, and any circle passing through both the north pole an ...