INVARIANCE OF DOMAIN AND THE JORDAN CURVE THEOREM
... an alternative definition of simply connected space. 3. Covering Spaces and the Fundamental Group of S 1 In algebraic topology, the notion of covering space is a very powerful tool. Here we are going to recall the definition and give the fundamental group of S 1 as an example. Definition 3.1. Let E ...
... an alternative definition of simply connected space. 3. Covering Spaces and the Fundamental Group of S 1 In algebraic topology, the notion of covering space is a very powerful tool. Here we are going to recall the definition and give the fundamental group of S 1 as an example. Definition 3.1. Let E ...
CONNECTIVE SPACES 1. Connective Spaces 1.1. Introduction. As
... 1.1. Introduction. As a topological concept connectedness is of somewhat different character than most other important properties, such as the covering properties, studied in the category TOP. Its aim is to topologically explain the intuitive notion of continuity of a point set. Roughly speaking, a ...
... 1.1. Introduction. As a topological concept connectedness is of somewhat different character than most other important properties, such as the covering properties, studied in the category TOP. Its aim is to topologically explain the intuitive notion of continuity of a point set. Roughly speaking, a ...
On function field Mordell-Lang and Manin-Mumford
... Definition 1.8. We will say that XA has quantifier elimination or QE, if T h(XA ) has quantifier elimination in the language above. It is clear from this definition that: Remark 1.9. XA has QE if and only if whenever Y is a relatively A-definable subset of X n+1 then the projection of Y to X n is re ...
... Definition 1.8. We will say that XA has quantifier elimination or QE, if T h(XA ) has quantifier elimination in the language above. It is clear from this definition that: Remark 1.9. XA has QE if and only if whenever Y is a relatively A-definable subset of X n+1 then the projection of Y to X n is re ...
The fundamental groupoid as a topological
... A:n(X, x)-+G{x}. Corollary 6. Let X be path-connected and x e X. The following conditions are equivalent. (i) StGx is path-connected. (ii) A: n(X, x)-+G{x} is surjective. (iii) 5* : n(G, lx)^>n(X, x) is surjective. Proof. These follow immediately from the exact homotopy sequences of the fibrations d ...
... A:n(X, x)-+G{x}. Corollary 6. Let X be path-connected and x e X. The following conditions are equivalent. (i) StGx is path-connected. (ii) A: n(X, x)-+G{x} is surjective. (iii) 5* : n(G, lx)^>n(X, x) is surjective. Proof. These follow immediately from the exact homotopy sequences of the fibrations d ...
General Topology of Ramified Coverings
... sheets over sufficiently small evenly covered open sets. A property of the map f suitable to replace local connectedness of the spaces would be a prescribed “slicing” [H; p. 97]. This is the only non-relative axiom that we introduce, for the sake of a reasonably simple exposition. The only separatio ...
... sheets over sufficiently small evenly covered open sets. A property of the map f suitable to replace local connectedness of the spaces would be a prescribed “slicing” [H; p. 97]. This is the only non-relative axiom that we introduce, for the sake of a reasonably simple exposition. The only separatio ...
... Throughout this paper (X, τ) and (Y, σ) stand for topological spaces with no separation axioms assumed, unless otherwise stated. Maki [3] introduced the notion of -sets in topological spaces. A -set is a set A which is equal to its kernel, that is, to the intersection of all open supersets of A. ...
Topology
... Q Definition 1.3 (box topology/product topology). On a product X := i∈I Xi of topological spaces Q • the products Qi∈I Ui of open subsets Ui ⊆ Xi form the basis of the box topology on X, while • the products i∈I Ui of open subsets Ui ⊆ Xi , where Ui ⊂ Xi may hold only for finitely many factors, form ...
... Q Definition 1.3 (box topology/product topology). On a product X := i∈I Xi of topological spaces Q • the products Qi∈I Ui of open subsets Ui ⊆ Xi form the basis of the box topology on X, while • the products i∈I Ui of open subsets Ui ⊆ Xi , where Ui ⊂ Xi may hold only for finitely many factors, form ...
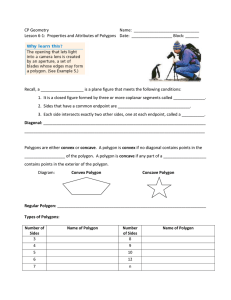
CP Geometry Name: Lesson 6-1: Properties and Attributes of
... Recall, a ___________________ is a plane figure that meets the following conditions: 1. It is a closed figure formed by three or more coplanar segments called ______________. 2. Sides that have a common endpoint are ________________________________. 3. Each side intersects exactly two other sides, o ...
... Recall, a ___________________ is a plane figure that meets the following conditions: 1. It is a closed figure formed by three or more coplanar segments called ______________. 2. Sides that have a common endpoint are ________________________________. 3. Each side intersects exactly two other sides, o ...
Bisector surfaces and circumscribed spheres of tetrahedra derived
... x, y, z ∈ R} on the points of space Sol = {(a, b, c) : a, b, c ∈ R}. These translations are not commutative, in general. Here we can consider L as projective collineation group with right actions in homogeneous coordinates as usual in classical affine-projective geometry. We will use the Cartesian h ...
... x, y, z ∈ R} on the points of space Sol = {(a, b, c) : a, b, c ∈ R}. These translations are not commutative, in general. Here we can consider L as projective collineation group with right actions in homogeneous coordinates as usual in classical affine-projective geometry. We will use the Cartesian h ...