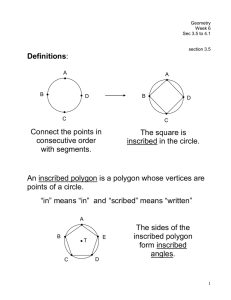
Definitions: An inscribed polygon is a polygon whose vertices are
... pencil are very sharp. 2. Lines and compass marks should look like eyelashes on the paper. These marks represent lines that have no width, so make the representations believable. Make light marks that can be erased if necessary. 3. Be neat. Carefully align your arcs and lines to pass through the cor ...
... pencil are very sharp. 2. Lines and compass marks should look like eyelashes on the paper. These marks represent lines that have no width, so make the representations believable. Make light marks that can be erased if necessary. 3. Be neat. Carefully align your arcs and lines to pass through the cor ...
January Regional Geometry Team: Question #1 Points P, Q, R, S
... Let A = The area of a rectangle with sides of 4x + 4 and 3x + 6 and perimeter = 90 Let B = The measure of the diagonal of a square that has an area of 250 Let C = The perimeter of a rhombus with diagonals that measure 18 and 24 Let D = The measure of the 8th angle in an octagon when the average of t ...
... Let A = The area of a rectangle with sides of 4x + 4 and 3x + 6 and perimeter = 90 Let B = The measure of the diagonal of a square that has an area of 250 Let C = The perimeter of a rhombus with diagonals that measure 18 and 24 Let D = The measure of the 8th angle in an octagon when the average of t ...
Triangle Unit: Day 6 - Greer Middle College
... Theorem: If two angles of a triangle are unequal, then the measures of the sides opposite these angles are also unequal, and the longer side is opposite the greater angle. i.e. the largest side is always across from the largest angle, and the smallest side is always across from the smallest angle. ...
... Theorem: If two angles of a triangle are unequal, then the measures of the sides opposite these angles are also unequal, and the longer side is opposite the greater angle. i.e. the largest side is always across from the largest angle, and the smallest side is always across from the smallest angle. ...
Homology Group - Computer Science, Stony Brook University
... All straight lines through the origin in ℝ3 form a two dimensional manifold, which is called the projective plane RP 2 . A projective plane can be obtained by identifying two antipodal points on the unit sphere. A projective plane with a hole is called a crosscap. π1 (RP 2 ) = {γ , e}. ...
... All straight lines through the origin in ℝ3 form a two dimensional manifold, which is called the projective plane RP 2 . A projective plane can be obtained by identifying two antipodal points on the unit sphere. A projective plane with a hole is called a crosscap. π1 (RP 2 ) = {γ , e}. ...
LessonPlanaccmathIoct31
... postulate). Give notes on properties in algebra and show how to prove algebraically. Using the same logic( deductive reasoning) , show how to prove triangles congruent using a flow chart. Worksheet on congruency for HW. TIX out the DOORGiven a triangle congruency – state all angles and sides congrue ...
... postulate). Give notes on properties in algebra and show how to prove algebraically. Using the same logic( deductive reasoning) , show how to prove triangles congruent using a flow chart. Worksheet on congruency for HW. TIX out the DOORGiven a triangle congruency – state all angles and sides congrue ...
Inequalites in Triangles
... Determine whether the measures 6.8, 7.2, and 5.1 can be lengths of the sides of a triangle. ...
... Determine whether the measures 6.8, 7.2, and 5.1 can be lengths of the sides of a triangle. ...
Geometry
... Write geometric proofs, including proofs by contradiction and proofs involving coordinate geometry. Use and compare a variety of ways to present deductive proofs, such as flow charts, paragraphs, two-column, and indirect proofs. ...
... Write geometric proofs, including proofs by contradiction and proofs involving coordinate geometry. Use and compare a variety of ways to present deductive proofs, such as flow charts, paragraphs, two-column, and indirect proofs. ...
Triangle reflection groups
... that T is a triangle in S2 . Since S2 is compact and the area of T is not 0, it follows that we need only a number of transformations to to cover S2 . Thus G is finite. Let G be finite and have the presentation above. Then there is a triangle T with angles kπ12 , kπ23 , kπ13 such that G is the refle ...
... that T is a triangle in S2 . Since S2 is compact and the area of T is not 0, it follows that we need only a number of transformations to to cover S2 . Thus G is finite. Let G be finite and have the presentation above. Then there is a triangle T with angles kπ12 , kπ23 , kπ13 such that G is the refle ...
Inequalities in One Triangle
... her hair. After she folds the handkerchief in half, the directions tell her to tie the two smaller angles of the triangle under her hair. If she folds the handkerchief with the dimensions shown, which two ends should she tie? ...
... her hair. After she folds the handkerchief in half, the directions tell her to tie the two smaller angles of the triangle under her hair. If she folds the handkerchief with the dimensions shown, which two ends should she tie? ...
Solutions Sheet 3
... in Z. By uniqueness of representatives, we can thus deduce that X Y represents F . For the functor in the exercise, it is natural to replace X Y by the set C(Y, X) of continuous functions Y → X, endowed with some topology. However, neither of the maps Z → C(Y, X), z 7→ fz and Z × Y → X, (z, y) 7→ g( ...
... in Z. By uniqueness of representatives, we can thus deduce that X Y represents F . For the functor in the exercise, it is natural to replace X Y by the set C(Y, X) of continuous functions Y → X, endowed with some topology. However, neither of the maps Z → C(Y, X), z 7→ fz and Z × Y → X, (z, y) 7→ g( ...
Geometry—Segment 2 Reference Sheet
... factor, a proportion, a ratio, or by a percent of change. ° Density: a ratio of mass to area or volume. ...
... factor, a proportion, a ratio, or by a percent of change. ° Density: a ratio of mass to area or volume. ...
Ch. 5 Review Key
... 22. a) If two sides of a triangle have lengths 9 and 15, can the third side be of length 6? NO! (9 + 6 = 15, and 2 sides must have a sum larger than the 3 rd side) b) Write an inequality that describes the length of the third side. 6 < x < 24 (If x is the biggest: 9 +15 > x, but if x is the smalles ...
... 22. a) If two sides of a triangle have lengths 9 and 15, can the third side be of length 6? NO! (9 + 6 = 15, and 2 sides must have a sum larger than the 3 rd side) b) Write an inequality that describes the length of the third side. 6 < x < 24 (If x is the biggest: 9 +15 > x, but if x is the smalles ...
B - Andre Van Delden
... her hair. After she folds the handkerchief in half, the directions tell her to tie the two smaller angles of the triangle under her hair. If she folds the handkerchief with the dimensions shown, which two ends should she tie? ...
... her hair. After she folds the handkerchief in half, the directions tell her to tie the two smaller angles of the triangle under her hair. If she folds the handkerchief with the dimensions shown, which two ends should she tie? ...
Basic Geometry - Area Perimeter Volume Surface Area
... Here are some other important definitions in understanding basic geometry. PLANES: the area defined by two-dimensional, flat surfaces. INTERSECT: to cross. PARALLEL: nonintersecting lines and/or planes. (The distance between straight, parallel lines/planes is the same at all locations. DEGREES: a ci ...
... Here are some other important definitions in understanding basic geometry. PLANES: the area defined by two-dimensional, flat surfaces. INTERSECT: to cross. PARALLEL: nonintersecting lines and/or planes. (The distance between straight, parallel lines/planes is the same at all locations. DEGREES: a ci ...
Triangle Inequalities in two triangles.notebook
... Triangle Inequalities in two triangles.notebook ...
... Triangle Inequalities in two triangles.notebook ...
Inequality and Triangle Lesson Plan
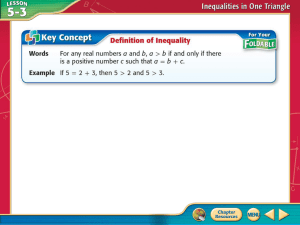
... > b if and only if there is a positive number c such that a = b + c. 2. Explain with numbers because with letters some students can get confused. Example: 6 > 4 because 6 = 4+2 3. Have students turn to the properties of inequalities on page 247 of text book. 4. These inequality properties are ones t ...
... > b if and only if there is a positive number c such that a = b + c. 2. Explain with numbers because with letters some students can get confused. Example: 6 > 4 because 6 = 4+2 3. Have students turn to the properties of inequalities on page 247 of text book. 4. These inequality properties are ones t ...
Systolic geometry

In mathematics, systolic geometry is the study of systolic invariants of manifolds and polyhedra, as initially conceived by Charles Loewner and developed by Mikhail Gromov, Michael Freedman, Peter Sarnak, Mikhail Katz, Larry Guth, and others, in its arithmetical, ergodic, and topological manifestations. See also a slower-paced Introduction to systolic geometry.