INDIAN INSTITUTE OF SCIENCE EDUCATION AND RESEARCH
... Biology Major . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Chemistry Major . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mathematics Major . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Physics Major . . ...
... Biology Major . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Chemistry Major . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mathematics Major . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Physics Major . . ...
Differential Forms and Electromagnetic Field Theory
... the unit spaced surfaces. A path from (0, 0, 0) to (0.25, 0, 0), for example, crosses 0.25 surfaces. We can also think of dx as a one-form in the plane. In this case, the picture becomes a series of lines perpendicular to the x-axis spaced a unit distance apart, as shown in Figure 2(b). Graphically, ...
... the unit spaced surfaces. A path from (0, 0, 0) to (0.25, 0, 0), for example, crosses 0.25 surfaces. We can also think of dx as a one-form in the plane. In this case, the picture becomes a series of lines perpendicular to the x-axis spaced a unit distance apart, as shown in Figure 2(b). Graphically, ...
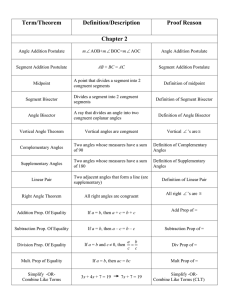
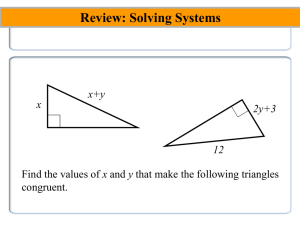
Triangle Congruence Theorems
... Side – Angle – Side Congruence: If, in two triangles, two sides and the included angle (formed by the two sides) are congruent, then the triangles are congruent. ...
... Side – Angle – Side Congruence: If, in two triangles, two sides and the included angle (formed by the two sides) are congruent, then the triangles are congruent. ...
Theorem - eGurukul
... Let us recall the procedure of proving a theorem logically. Observe the following flow chart. Consider/take a statement or the Enunciation of the theorem ...
... Let us recall the procedure of proving a theorem logically. Observe the following flow chart. Consider/take a statement or the Enunciation of the theorem ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.