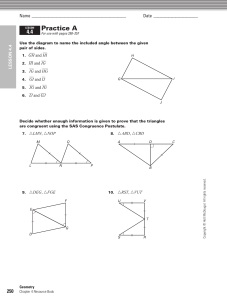
4.4 Proving Triangles are Congruent: ASA and AAS
... A. In addition to the angles and segments that are marked, EGF JGH by the Vertical Angles Theorem. Two pairs of corresponding angles and one pair of corresponding sides are congruent. You can use the AAS Congruence Theorem to prove that ∆EFG ∆JHG. ...
... A. In addition to the angles and segments that are marked, EGF JGH by the Vertical Angles Theorem. Two pairs of corresponding angles and one pair of corresponding sides are congruent. You can use the AAS Congruence Theorem to prove that ∆EFG ∆JHG. ...
MODULE MAPS OVER LOCALLY COMPACT QUANTUM GROUPS
... M (C0 (G)). This is a quite general result, which covers all Kac algebras, though we still do not know whether it holds for all quantum groups. See [56, 58] for some co-amenable cases, where LU C(G) was also shown to be a C ∗ -algebra. Let W AP (G) be the space of weakly almost periodic functionals ...
... M (C0 (G)). This is a quite general result, which covers all Kac algebras, though we still do not know whether it holds for all quantum groups. See [56, 58] for some co-amenable cases, where LU C(G) was also shown to be a C ∗ -algebra. Let W AP (G) be the space of weakly almost periodic functionals ...
Delft University of Technology
... the micro and nano meter range are trapped by the surrounding electromagnetic fields. The first observation of this trapping force using a single beam was in the mid 1980s [1]. The trapping of these small particles has a wide range of applications. One can think of separation of particles with diffe ...
... the micro and nano meter range are trapped by the surrounding electromagnetic fields. The first observation of this trapping force using a single beam was in the mid 1980s [1]. The trapping of these small particles has a wide range of applications. One can think of separation of particles with diffe ...
4.5 Prove Triangles Congruent by ASA and AAS
... a. There is not enough information to prove the triangles are congruent, because no sides are known to be congruent. b. Two pairs of angles and a non-included pair of sides are congruent. The triangles are congruent by the AAS Congruence Theorem . c. The vertical angles are congruent, so two pairs o ...
... a. There is not enough information to prove the triangles are congruent, because no sides are known to be congruent. b. Two pairs of angles and a non-included pair of sides are congruent. The triangles are congruent by the AAS Congruence Theorem . c. The vertical angles are congruent, so two pairs o ...
Geometry Common Core
... some students develop Euclidean and other geometries carefully from a small set of axioms. The concepts of congruence, similarity, and symmetry can be understood from the perspective of geometric transformation. Fundamental are the rigid motions: translations, rotations, reflections, and combination ...
... some students develop Euclidean and other geometries carefully from a small set of axioms. The concepts of congruence, similarity, and symmetry can be understood from the perspective of geometric transformation. Fundamental are the rigid motions: translations, rotations, reflections, and combination ...
Spiral Symmetry on the TI-92
... We can also express the spiral in terms of the base e: r (θ ) = aeθ ln( µ0 ) . The quantity ln( µ 0 ) has a geometric interpretation. Theorem: The equation of the spiral can be written in the form r (θ ) = aeθ cot(φ ) , where φ = cot −1 (ln( µ 0 )) is the angle between the radius vector to a point o ...
... We can also express the spiral in terms of the base e: r (θ ) = aeθ ln( µ0 ) . The quantity ln( µ 0 ) has a geometric interpretation. Theorem: The equation of the spiral can be written in the form r (θ ) = aeθ cot(φ ) , where φ = cot −1 (ln( µ 0 )) is the angle between the radius vector to a point o ...
Week 7
... MCC9-12.G.CO.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equ ...
... MCC9-12.G.CO.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equ ...
pdf file - Gandalf Lechner
... has a good physical motivation. On the other hand, it has the potential of being applicable to quantum field theories on general curved spacetimes because it does not involve any objects which exist only for Minkowski space theories. In this article, we study a (variant of the) modular nuclearity co ...
... has a good physical motivation. On the other hand, it has the potential of being applicable to quantum field theories on general curved spacetimes because it does not involve any objects which exist only for Minkowski space theories. In this article, we study a (variant of the) modular nuclearity co ...
A Foundation for Geometry
... Example 4.3 (Lines on a sphere). Let X be a sphere and suppose that we restrict travel to the surface of the sphere. Then the distance between two points P and Q on the sphere is measured along the great circle of the sphere which passes through the two points. A great circle is a circle on the sphe ...
... Example 4.3 (Lines on a sphere). Let X be a sphere and suppose that we restrict travel to the surface of the sphere. Then the distance between two points P and Q on the sphere is measured along the great circle of the sphere which passes through the two points. A great circle is a circle on the sphe ...
AND RANDOM MOSAICS ON A PLANE
... contraction of a homogeneous random field of points having a Poisson distribution with parameter A in the whole space (x, y, 'p). Let us put ',,(X) = a, where a is a constant. Such an h.i.r.f.s. is called a field of segments of length a, scattered independently in the plane. EXAMPLE 2. Let Y be some ...
... contraction of a homogeneous random field of points having a Poisson distribution with parameter A in the whole space (x, y, 'p). Let us put ',,(X) = a, where a is a constant. Such an h.i.r.f.s. is called a field of segments of length a, scattered independently in the plane. EXAMPLE 2. Let Y be some ...
10/29/2007 Julia Velkovska PHY 340a
... • Major victory of theoretical physics was finding a structure which could include electromagnetism and weak forces in a single set of fields • If we assume g=e, and measure G (the strength of the weak interactions) we can extract M ...
... • Major victory of theoretical physics was finding a structure which could include electromagnetism and weak forces in a single set of fields • If we assume g=e, and measure G (the strength of the weak interactions) we can extract M ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.