Tensorial spacetime geometries and background
... that the corresponding field theory be predictive and that there be a well-defined notion of observers and positive energy. From that we will find that there are four conditions that must be fulfilled by every tensorial background in order to be a viable spacetime structure which will then be called ...
... that the corresponding field theory be predictive and that there be a well-defined notion of observers and positive energy. From that we will find that there are four conditions that must be fulfilled by every tensorial background in order to be a viable spacetime structure which will then be called ...
Magnetic materials: domain walls, vortices, and bubbles (lecture
... 1. THE MAGNETIZATION VECTOR AND THE LANDAU-LIFSHITZ EQUATION ...
... 1. THE MAGNETIZATION VECTOR AND THE LANDAU-LIFSHITZ EQUATION ...
Document
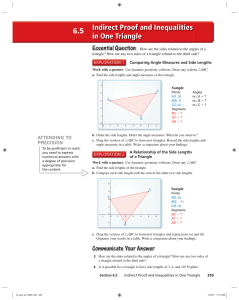
... 1. Write a conditional from the sentence “An isosceles triangle has two congruent sides.” If a ∆ is isosc., then it has 2 sides. 2. Write the contrapositive of the conditional “If it is Tuesday, then John has a piano lesson.” If John does not have a piano lesson, then it is not Tuesday. 3. Show th ...
... 1. Write a conditional from the sentence “An isosceles triangle has two congruent sides.” If a ∆ is isosc., then it has 2 sides. 2. Write the contrapositive of the conditional “If it is Tuesday, then John has a piano lesson.” If John does not have a piano lesson, then it is not Tuesday. 3. Show th ...
Weak-Field General Relativity Compared with
... The concept of vectors is familiar but takes on a different cast in relativity. Vectors exist at a single point in spacetime and can be thought of as tangent vectors at that point, thus the collection of all vectors at a given point, the tangent space, all lie on some subspace which is tangent at th ...
... The concept of vectors is familiar but takes on a different cast in relativity. Vectors exist at a single point in spacetime and can be thought of as tangent vectors at that point, thus the collection of all vectors at a given point, the tangent space, all lie on some subspace which is tangent at th ...
Postulates and Theorems
... If a triangle inscribed in a circle is a right triangle, then the hypotenuse is a diameter of the circle. If a side of a triangle inscribed in a circle is a diameter of the circle, then the triangle is a right triangle. (p. 615) ...
... If a triangle inscribed in a circle is a right triangle, then the hypotenuse is a diameter of the circle. If a side of a triangle inscribed in a circle is a diameter of the circle, then the triangle is a right triangle. (p. 615) ...
Copyright © by Holt, Rinehart and Winston
... Name _______________________________________ Date ___________________ Class __________________ ...
... Name _______________________________________ Date ___________________ Class __________________ ...
High School Geometry Correlation of the ALEKS course High
... G-CO.10: Using methods of proof including direct, indirect, and counter examples to prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is ...
... G-CO.10: Using methods of proof including direct, indirect, and counter examples to prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.