Classical Field Theory
... place ourselves at ~x′ = (0, 1, 0) and ask what the old field looked like where we have come from at R−1 (0, 1, 0) = (1, 0, 0). This R−1 is the origin of the inverse transformation. In other words, the transformed field, evaluated at the new (boosted) point x, must give the same result as the origin ...
... place ourselves at ~x′ = (0, 1, 0) and ask what the old field looked like where we have come from at R−1 (0, 1, 0) = (1, 0, 0). This R−1 is the origin of the inverse transformation. In other words, the transformed field, evaluated at the new (boosted) point x, must give the same result as the origin ...
Lagrangian and Hamiltonian forms of the Electromagnetic Interaction
... Note that in the last line, the first term corresponds to k , i and the second term to i, k . These are the only possibilities, since ijk must all be different (otherwise ijk 0 ). The student should convince himself/herself that the last line of (1.9) is indeed identical to the l ...
... Note that in the last line, the first term corresponds to k , i and the second term to i, k . These are the only possibilities, since ijk must all be different (otherwise ijk 0 ). The student should convince himself/herself that the last line of (1.9) is indeed identical to the l ...
Introduction to Electromagnetism
... Newton’s laws Vectors, derivatives Coordinate systems Force and momentum Energies ...
... Newton’s laws Vectors, derivatives Coordinate systems Force and momentum Energies ...
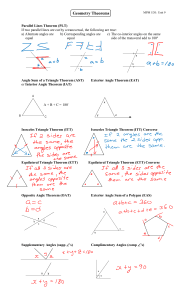
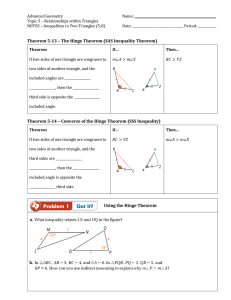
Geometry Theorem Acronyms
... Parallel Lines Theorem (PLT) If two parallel lines are cut by a transversal, the following are true: a) Alternate angles are b) Corresponding angles are c) The co-interior angles on the same equal equal side of the transveral add to 180º ...
... Parallel Lines Theorem (PLT) If two parallel lines are cut by a transversal, the following are true: a) Alternate angles are b) Corresponding angles are c) The co-interior angles on the same equal equal side of the transveral add to 180º ...
Document
... Remark 1. The vectorΩis called the ground, or vacuum state, since it has lowest energy, and physicists often shift the Hamiltonian by a constant, so that the energy of this state is zero (i.e. there is no matter). Remark 2. Physicists usually write the inner product (v,Aw) as < v|A|w >. In particula ...
... Remark 1. The vectorΩis called the ground, or vacuum state, since it has lowest energy, and physicists often shift the Hamiltonian by a constant, so that the energy of this state is zero (i.e. there is no matter). Remark 2. Physicists usually write the inner product (v,Aw) as < v|A|w >. In particula ...
Relativistic mechanics - IIS Severi
... We saw that x and t aren’t invariant quantities as regards Lorentz’s Transformation. If we think to L-T as transformation of coordinates in a 4-D space, then we have to find what is the geometrical characteristic (invariant) in such a 4-D space – the so-called Minkowsky’s space-time – . ...
... We saw that x and t aren’t invariant quantities as regards Lorentz’s Transformation. If we think to L-T as transformation of coordinates in a 4-D space, then we have to find what is the geometrical characteristic (invariant) in such a 4-D space – the so-called Minkowsky’s space-time – . ...
1.4 Particle physics - McMaster Physics and Astronomy
... its corresponding action, S. The Lagrangian that describes fundamental particles is not as simple as the Lagrangian of Eq. (1.15), its form and meaning is shaped by Lorentz symmetry and quantum mechanics, and the generalized coordinates do not represent the position of a particle, but rather fields ...
... its corresponding action, S. The Lagrangian that describes fundamental particles is not as simple as the Lagrangian of Eq. (1.15), its form and meaning is shaped by Lorentz symmetry and quantum mechanics, and the generalized coordinates do not represent the position of a particle, but rather fields ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.