homework 2, due October 3rd
... Consider a particle described at some particular instant of time by the wave function ψ(x) = Ae−ax . 1. Determine A so ψ is normalized. 2. Compute hxi, hx2 i and σx2 = h(x − hxi)2 i. 3. Compute hpi, hp2 i and σp2 = h(p − hpi)2 i. 4. Show that by changing a one can make either σx2 or σp2 small, but n ...
... Consider a particle described at some particular instant of time by the wave function ψ(x) = Ae−ax . 1. Determine A so ψ is normalized. 2. Compute hxi, hx2 i and σx2 = h(x − hxi)2 i. 3. Compute hpi, hp2 i and σp2 = h(p − hpi)2 i. 4. Show that by changing a one can make either σx2 or σp2 small, but n ...
Linear-Response Theory, Kubo Formula, Kramers
... (Actually, because of causality, the upper integration limit, ∞, can be replaced by t, and the lower one, t0 , by −∞, if the perturbation is switched on adiabatically.) The function XÂ,B̂ (t − t′ ) is (apart from a minus sign) identical with the retarded Green’s function GÂ,B̂ (t − t′ ), and, whic ...
... (Actually, because of causality, the upper integration limit, ∞, can be replaced by t, and the lower one, t0 , by −∞, if the perturbation is switched on adiabatically.) The function XÂ,B̂ (t − t′ ) is (apart from a minus sign) identical with the retarded Green’s function GÂ,B̂ (t − t′ ), and, whic ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... FIRST SEMESTER – NOVEMBER 2010 PH 1812 - ELECTRODYNAMICS Date : 30-10-10 Time : 1:00 - 4:00 ...
... FIRST SEMESTER – NOVEMBER 2010 PH 1812 - ELECTRODYNAMICS Date : 30-10-10 Time : 1:00 - 4:00 ...
Slide 1
... Should the selected orientation of the x-axis matter? As far as the form of the equations of motion? (all derivable from a Lagrangian) As far as the predictions those equations make? Any calculable quantities/outcpome/results? Should the selected position of the coordinate origin matter? If it “doe ...
... Should the selected orientation of the x-axis matter? As far as the form of the equations of motion? (all derivable from a Lagrangian) As far as the predictions those equations make? Any calculable quantities/outcpome/results? Should the selected position of the coordinate origin matter? If it “doe ...
AAS Theorem - Math Story
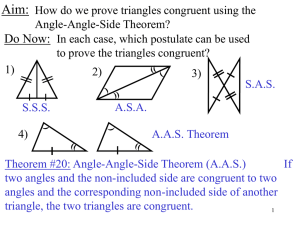
... Aim: How do we prove triangles congruent using the Angle-Angle-Side Theorem? Do Now: In each case, which postulate can be used to prove the triangles congruent? ...
... Aim: How do we prove triangles congruent using the Angle-Angle-Side Theorem? Do Now: In each case, which postulate can be used to prove the triangles congruent? ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.