Tutorial 1
... susceptibility. Hence find the real and imaginary parts of the refractive index, n = n1 jn2, as functions of the wave frequency . Sketch a plot of n1 and n2 as a function of the wave frequency . Indicate on your plot regions of normal and anomalous dispersion. Describe how the shape of the plot ...
... susceptibility. Hence find the real and imaginary parts of the refractive index, n = n1 jn2, as functions of the wave frequency . Sketch a plot of n1 and n2 as a function of the wave frequency . Indicate on your plot regions of normal and anomalous dispersion. Describe how the shape of the plot ...
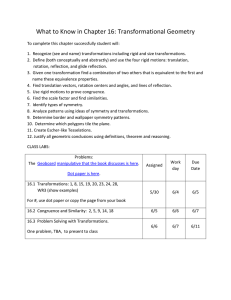
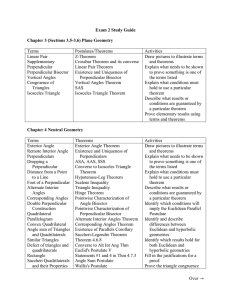
transformationunit
... 3. Given one transformation find a combination of two others that is equivalent to the first and name these equivalence properties. 4. Find translation vectors, rotation centers and angles, and lines of reflection. 5. Use rigid motions to prove congruence. 6. Find the scale factor and find similarit ...
... 3. Given one transformation find a combination of two others that is equivalent to the first and name these equivalence properties. 4. Find translation vectors, rotation centers and angles, and lines of reflection. 5. Use rigid motions to prove congruence. 6. Find the scale factor and find similarit ...
Variational Principles and Lagrangian Mechanics
... The amplitude for a given path ~r(t) is of the form e h̄ S[~r] , where S[~r] is the action functional for the trajectory.† The action functional assigns a number to each path ~r(t) connecting ~r1 to ~r2 . The specific way in which the action assigns numbers to paths depends upon the physics (degrees ...
... The amplitude for a given path ~r(t) is of the form e h̄ S[~r] , where S[~r] is the action functional for the trajectory.† The action functional assigns a number to each path ~r(t) connecting ~r1 to ~r2 . The specific way in which the action assigns numbers to paths depends upon the physics (degrees ...
File
... constant velocity will continue in motion unless acted upon by some net external force. Newton’s second law: Introduces force (F) as responsible for the the change in linear momentum (p): ...
... constant velocity will continue in motion unless acted upon by some net external force. Newton’s second law: Introduces force (F) as responsible for the the change in linear momentum (p): ...
lect3
... Consider a flux of particles, momentum ħk, energy E= ħ2k2/2m approaching a barrier, height V0 (V0 > E), width a. ...
... Consider a flux of particles, momentum ħk, energy E= ħ2k2/2m approaching a barrier, height V0 (V0 > E), width a. ...
1 (12 points) Answer the following questions. (1) A central force F r
... In the isothermal expansion process of Method A, what is the amount of work done by the gas (ΔW), the quantity of heat acquired by the gas (ΔQ), and the change in entropy of the gas (ΔS )? Include signs in your answers. In the adiabatic expansion process of Method B, what is the amount of work done ...
... In the isothermal expansion process of Method A, what is the amount of work done by the gas (ΔW), the quantity of heat acquired by the gas (ΔQ), and the change in entropy of the gas (ΔS )? Include signs in your answers. In the adiabatic expansion process of Method B, what is the amount of work done ...
i∂φ
... This is a direct consequence of the quantization of (canonical) angular momentum. Since φ̇ is neither the time derivative of a welldefined operator, nor the commutator of the Hamiltonian with one, there is no contradiction. *(The half-odd integer case requires special consideration.) ...
... This is a direct consequence of the quantization of (canonical) angular momentum. Since φ̇ is neither the time derivative of a welldefined operator, nor the commutator of the Hamiltonian with one, there is no contradiction. *(The half-odd integer case requires special consideration.) ...
1 Classical Mechanics
... The formulation of quantum mechanics by Hamilton is the most useful for seeing the connections between classical and quantum mechanics. Schrödinger made brilliant use of Hamilton’s ideas in writing down his wave equation. Dirac and Feynman used Hamiton’s princple to formulate the path integral appr ...
... The formulation of quantum mechanics by Hamilton is the most useful for seeing the connections between classical and quantum mechanics. Schrödinger made brilliant use of Hamilton’s ideas in writing down his wave equation. Dirac and Feynman used Hamiton’s princple to formulate the path integral appr ...
Principles of Computer Architecture Dr. Mike Frank
... • Classical mechanics can be expressed most generally and concisely in the Lagrangian and Hamiltonian formulations. • Based on simple functions of the system state: – Lagrangian: Kinetic minus potential energy. – Hamiltonian: Kinetic plus potential energy. ...
... • Classical mechanics can be expressed most generally and concisely in the Lagrangian and Hamiltonian formulations. • Based on simple functions of the system state: – Lagrangian: Kinetic minus potential energy. – Hamiltonian: Kinetic plus potential energy. ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.