A quadrilateral that has one set of parallel sides is called a . For this
... because of the _____________ property. Furthermore,
... because of the _____________ property. Furthermore,
Possible large-N fixed-points and naturalness for O(N) scalar fields
... symmetric, broken to custodial O(3) symmetry by the scalar vev). There is a precedent for this. 3D quantum λ|φ|6 theory is scale invariant at N = ∞ for any λ, though whether there is any non-trivial fixed point for finite N is unclear [19, 20]. In d = 4, an idea to use the N → ∞ limit to construct a ...
... symmetric, broken to custodial O(3) symmetry by the scalar vev). There is a precedent for this. 3D quantum λ|φ|6 theory is scale invariant at N = ∞ for any λ, though whether there is any non-trivial fixed point for finite N is unclear [19, 20]. In d = 4, an idea to use the N → ∞ limit to construct a ...
Chapter 4 - Mater Academy Charter Middle/ High
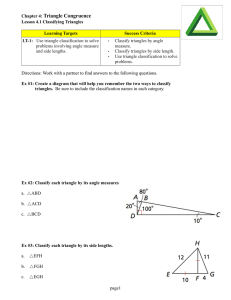
... • PAGE 231 #11-14, 17, 24-26, 35-38 • PAGE 238 #13, 16-18, 25, 32-35 ...
... • PAGE 231 #11-14, 17, 24-26, 35-38 • PAGE 238 #13, 16-18, 25, 32-35 ...
electromagnetic energy-momentum tensor within material media
... For the main part we discuss gedanken experiments which have been pu t forward to support either MINxowSKI ' s or ABRAHAM ' S tensor, and show ho w these situations are to be explained with the use of the formerly rejecte d alternative . In the remaining part of the section we mainly discuss som e a ...
... For the main part we discuss gedanken experiments which have been pu t forward to support either MINxowSKI ' s or ABRAHAM ' S tensor, and show ho w these situations are to be explained with the use of the formerly rejecte d alternative . In the remaining part of the section we mainly discuss som e a ...
AN INTRODUCTION TO THE MEAN CURVATURE FLOW Contents
... In other words, we get that the mean curvature flow is the corresponding gradient flow for the area functional: The Mean Curvature Flow is the flow of steepest decrease of surface area. Moreover, we also have a nice maximum principle for this particular diffusion equation. Theorem (Maximum/Compariso ...
... In other words, we get that the mean curvature flow is the corresponding gradient flow for the area functional: The Mean Curvature Flow is the flow of steepest decrease of surface area. Moreover, we also have a nice maximum principle for this particular diffusion equation. Theorem (Maximum/Compariso ...
congruent triangles
... 5.1 Bisectors of a Triangle Concurrency of Perpendicular Bisectors of a Triangle: Perpendicular bisectors of a triangle are all concurrent at a point called the circumcenter. This point is equidistant from the all the vertices in the triangle. ...
... 5.1 Bisectors of a Triangle Concurrency of Perpendicular Bisectors of a Triangle: Perpendicular bisectors of a triangle are all concurrent at a point called the circumcenter. This point is equidistant from the all the vertices in the triangle. ...
Chapter 4: Triangle Congruence
... Position each figure in the coordinate plane and give the coordinates of each vertex A. A rectangle with width m and length twice the B. A right triangle with legs of lengths s and r. width. ...
... Position each figure in the coordinate plane and give the coordinates of each vertex A. A rectangle with width m and length twice the B. A right triangle with legs of lengths s and r. width. ...
Similarity - MrsMcFadin
... Given two similar polygons. Find the missing side length. Redraw one of the polygons so corresponding sides match up (if needed) Determine the scale factor Set up a proportion and solve for the missing side length ...
... Given two similar polygons. Find the missing side length. Redraw one of the polygons so corresponding sides match up (if needed) Determine the scale factor Set up a proportion and solve for the missing side length ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.