Monomior: is a constant variable or a porduct of a constant and one
... Prime number: positive integers which has exactly 2 divisor Compostive numbers: positive integers which have more than 2 divisiors Common factorization: every number can be composed as a product of a prime number G.C.D.: of two or more positive integers is the greatest positive integer that is a div ...
... Prime number: positive integers which has exactly 2 divisor Compostive numbers: positive integers which have more than 2 divisiors Common factorization: every number can be composed as a product of a prime number G.C.D.: of two or more positive integers is the greatest positive integer that is a div ...
Applied Geometry - South Harrison County R2
... Proving Angle Relationships Objective: Write proofs involving supplementary angles. Write proofs involving congruent and right angles. ...
... Proving Angle Relationships Objective: Write proofs involving supplementary angles. Write proofs involving congruent and right angles. ...
4.2 Angle Relationships in Triangles Sum Theorem: The sum of the
... 1. The measure of one acute angle of a right triangle is one-fourth the measure of the other acute angle. Find the angles. ...
... 1. The measure of one acute angle of a right triangle is one-fourth the measure of the other acute angle. Find the angles. ...
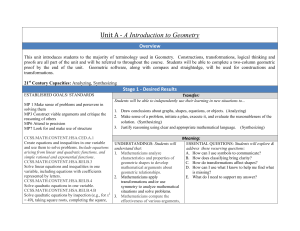
Unit A - A Introduction to Geometry
... D. How can I use what I know to help me find what variable, including equations with coefficients geometric relationships. is missing? represented by letters. 2. Mathematicians apply E. What do I need to support my answer? CCSS.MATH.CONTENT.HSA.REI.B.4 transformations and/or use Solve quadratic equa ...
... D. How can I use what I know to help me find what variable, including equations with coefficients geometric relationships. is missing? represented by letters. 2. Mathematicians apply E. What do I need to support my answer? CCSS.MATH.CONTENT.HSA.REI.B.4 transformations and/or use Solve quadratic equa ...
Converse of the Pythagorean Theorem
... Provide instruction on writing mathematical explanations, justifications, and proofs. Encourage the student to first consider the statement to be proven. Next, ask the student to examine the assumptions and then formulate an overall strategy. Make clear that every step must be justified with mathema ...
... Provide instruction on writing mathematical explanations, justifications, and proofs. Encourage the student to first consider the statement to be proven. Next, ask the student to examine the assumptions and then formulate an overall strategy. Make clear that every step must be justified with mathema ...
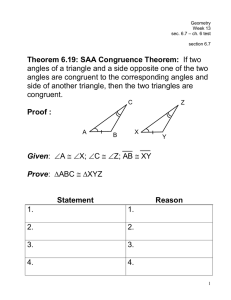
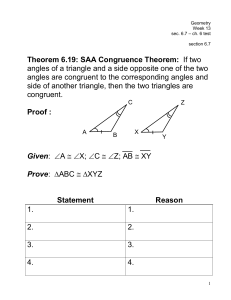
week13
... Given: A X; C Z; AB XY Prove: ABC XYZ Statement 1. A X; C Z; AB XY 2. B Y ...
... Given: A X; C Z; AB XY Prove: ABC XYZ Statement 1. A X; C Z; AB XY 2. B Y ...
Lie point symmetries: An alternative approach to wave
... of wave-functions or the odd series. When one is at a higher state, the symmetries Γ2 and Γ4 can both be used as annihilation operators with the former annihilating in steps of two. The energy eigenvalue comes from the single remaining nontrivial symmetry, videlicet Γ1 . The various methods for the ...
... of wave-functions or the odd series. When one is at a higher state, the symmetries Γ2 and Γ4 can both be used as annihilation operators with the former annihilating in steps of two. The energy eigenvalue comes from the single remaining nontrivial symmetry, videlicet Γ1 . The various methods for the ...
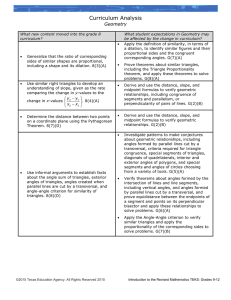
Curriculum Analysis
... intersection of lines and line segments, including vertical angles, and angles formed by parallel lines cut by a transversal, and prove equidistance between the endpoints of a segment and points on its perpendicular bisector and apply these relationships to solve problems. G(6)(A) ...
... intersection of lines and line segments, including vertical angles, and angles formed by parallel lines cut by a transversal, and prove equidistance between the endpoints of a segment and points on its perpendicular bisector and apply these relationships to solve problems. G(6)(A) ...
3.1 Energy in the field - Massachusetts Institute of Technology
... We can deduce one further important property of equipotential surfaces. By definition, the potential is constant on them, so they define the directions along which the potential does not change at all. The gradient, by contrast, defines the direction along which the potential changes the most! If yo ...
... We can deduce one further important property of equipotential surfaces. By definition, the potential is constant on them, so they define the directions along which the potential does not change at all. The gradient, by contrast, defines the direction along which the potential changes the most! If yo ...
Section 5.5: Inequalities in Triangles
... Ex: List the sides of the angles from longest to shortest K ...
... Ex: List the sides of the angles from longest to shortest K ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.