1.7 Momentum
... there is no external force. In practice, if the time of collision is small enough, we can ignore the external force and assume momentum conservation. For example, when a racket strikes a tennis ball, the effect due to gravitational force (external force) is neglected since the time of impact is very ...
... there is no external force. In practice, if the time of collision is small enough, we can ignore the external force and assume momentum conservation. For example, when a racket strikes a tennis ball, the effect due to gravitational force (external force) is neglected since the time of impact is very ...
2nd 9 weeks
... a. A dilation takes a line not passing through the center of the dilation in the coordinate plane. to a parallel line, and leaves a line passing through the center I can verify that when a side passes through the center of dilation, the unchanged. side and its image lie on the same line. b. The dila ...
... a. A dilation takes a line not passing through the center of the dilation in the coordinate plane. to a parallel line, and leaves a line passing through the center I can verify that when a side passes through the center of dilation, the unchanged. side and its image lie on the same line. b. The dila ...
classical theoretical physics II
... As a prelude to our discussion of the full set of Maxwell equations, let us address a question which, in principle, should have been answered in the previous chapter: What is the energy stored in a static magnetic field? In section ??, the analogous question for the electric field was answered in a ...
... As a prelude to our discussion of the full set of Maxwell equations, let us address a question which, in principle, should have been answered in the previous chapter: What is the energy stored in a static magnetic field? In section ??, the analogous question for the electric field was answered in a ...
Concepts 6
... Each statement must have a reason to justify it. Properties, postulates, definitions, and theorems are used as reasons in a proof. ...
... Each statement must have a reason to justify it. Properties, postulates, definitions, and theorems are used as reasons in a proof. ...
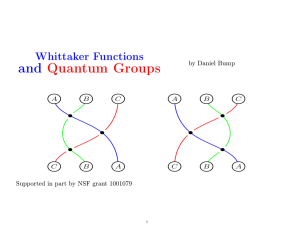
Whittaker Functions and Quantum Groups
... We will soon enter territory where each Cartan type must be handled individually, and although results are available for other Cartan types we will restrict ourselves to Type A, that is, GL(n). Here is the Casselman-Shalika formula for GL(n). (It was proved earlier by Shintani for this case.) If G = ...
... We will soon enter territory where each Cartan type must be handled individually, and although results are available for other Cartan types we will restrict ourselves to Type A, that is, GL(n). Here is the Casselman-Shalika formula for GL(n). (It was proved earlier by Shintani for this case.) If G = ...
Proofs of the inscribed angle theorem
... Solution. Without limiting the generality suppose that radius of circumcircle r = 1. Then the arc length is equal to the corresponding central angle. In accordance with the denoting in Figure 14 we get So triangle AID is isosceles, ...
... Solution. Without limiting the generality suppose that radius of circumcircle r = 1. Then the arc length is equal to the corresponding central angle. In accordance with the denoting in Figure 14 we get So triangle AID is isosceles, ...
Chapter 3.6 Practice G and K Answers
... 4. Look at Exercise 3. Can you prove that △ABD ≅ △CDB without using the Hypotenuse-Leg Theorem? Explain. Yes; answers may vary. Sample: You know that AB @ CD from the diagram and DB @ BD by the Reflexive Property of Congruence. Because the triangles are right triangles, the sides are related by the ...
... 4. Look at Exercise 3. Can you prove that △ABD ≅ △CDB without using the Hypotenuse-Leg Theorem? Explain. Yes; answers may vary. Sample: You know that AB @ CD from the diagram and DB @ BD by the Reflexive Property of Congruence. Because the triangles are right triangles, the sides are related by the ...
Section 1.3 - TTU Physics
... deal with. No general method to treat problems with Non-Holonomic constraints. Treat on case-by-case basis. • In special cases of Non-Holonomic constraints, when constraint is expressed in differential form (as in example), can use method of Lagrange multipliers along with Lagrange’s eqtns (later). ...
... deal with. No general method to treat problems with Non-Holonomic constraints. Treat on case-by-case basis. • In special cases of Non-Holonomic constraints, when constraint is expressed in differential form (as in example), can use method of Lagrange multipliers along with Lagrange’s eqtns (later). ...
Transport Theory Breakdown of Onsager Symmetry in Neoclassical PFC/JA-82-31
... is much thinner than E. A layer width, AK, on the order of several percent of E, accounts for 80% of the effect. In contrast, the Ware effect T7If has equal contributions from all the trapped particles. Since the explicit bootstrap current T3 is uniformly small for all X, the underlying asymmetry in ...
... is much thinner than E. A layer width, AK, on the order of several percent of E, accounts for 80% of the effect. In contrast, the Ware effect T7If has equal contributions from all the trapped particles. Since the explicit bootstrap current T3 is uniformly small for all X, the underlying asymmetry in ...
Part I Linear Spaces
... One could think of this theorem as an example of a local to global principle for linear maps: as long as the local constraint is reasonable we could preserve it globally. Here we need homogeneity and convexity. Proof of the HB theorem in this generality uses Zorn’s lemma which is equivalent to the a ...
... One could think of this theorem as an example of a local to global principle for linear maps: as long as the local constraint is reasonable we could preserve it globally. Here we need homogeneity and convexity. Proof of the HB theorem in this generality uses Zorn’s lemma which is equivalent to the a ...
Teaching Geometry-dj
... 10. The pink sticks need to alternate properly with blues, and purples too, so there is a trick to inserting them. Rotate the above configuration away from you, so that you now hold orange vertically, looking down the future pink direction. Put your thumbs on the ends of the blue and purple sticks n ...
... 10. The pink sticks need to alternate properly with blues, and purples too, so there is a trick to inserting them. Rotate the above configuration away from you, so that you now hold orange vertically, looking down the future pink direction. Put your thumbs on the ends of the blue and purple sticks n ...
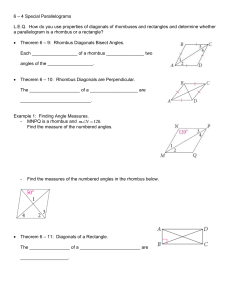
Geometry Standards with Learning Targets
... STANDARD 1: Tools of Geometry (Geometry Basics) (CCSS: G.CO.1, G.CO.12; 8-10 days) Students will be able to: a) Identify points, lines and planes and name them using correct notation b) Identify parts of a line (segments and rays) and name them using correct notation c) Use the definition of midpoin ...
... STANDARD 1: Tools of Geometry (Geometry Basics) (CCSS: G.CO.1, G.CO.12; 8-10 days) Students will be able to: a) Identify points, lines and planes and name them using correct notation b) Identify parts of a line (segments and rays) and name them using correct notation c) Use the definition of midpoin ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.