Geometry and measure
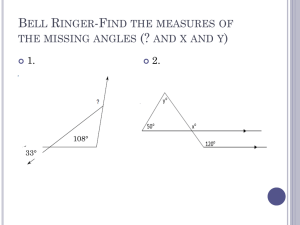
... 3.1 Lines and angles Angles and triangles An acute angle is between 0° and 90°. A right angle is exactly 90°. An obtuse angle is between 90° and 180°. A reflex angle is between 180° and 360°. The angles on a straight line add up to 180°. The angles at a point add up to 360°. The angles in a triangle ...
... 3.1 Lines and angles Angles and triangles An acute angle is between 0° and 90°. A right angle is exactly 90°. An obtuse angle is between 90° and 180°. A reflex angle is between 180° and 360°. The angles on a straight line add up to 180°. The angles at a point add up to 360°. The angles in a triangle ...
l - OPUS at UTS - University of Technology Sydney
... We note from (2.7) and (2.8) that all results obtained involving arctan (arctanh) can be expressed ...
... We note from (2.7) and (2.8) that all results obtained involving arctan (arctanh) can be expressed ...
What is an Angle
... A right angle is an angle measuring 90 degrees. Two lines or line segments that meet at a right angle are said to be perpendicular. Note that any two right angles are supplementary angles (a right angle is its own angle supplement). Example: The following angles are both right angles. ...
... A right angle is an angle measuring 90 degrees. Two lines or line segments that meet at a right angle are said to be perpendicular. Note that any two right angles are supplementary angles (a right angle is its own angle supplement). Example: The following angles are both right angles. ...
Slide 1
... 1. m1 = 120°, m2 = (60x)° Alt. Ext. s Thm.; m2 = 120° 2. m2 = (75x – 30)°, m3 = (30x + 60)° Corr. s Post.; m2 = 120°, m3 = 120° 3. m3 = (50x + 20)°, m4= (100x – 80)° Alt. Int. s Thm.; m3 = 120°, m4 =120° 4. m3 = (45x + 30)°, m5 = (25x + 10)° Same-Side Int. s Thm.; m3 = 120°, m5 =6 ...
... 1. m1 = 120°, m2 = (60x)° Alt. Ext. s Thm.; m2 = 120° 2. m2 = (75x – 30)°, m3 = (30x + 60)° Corr. s Post.; m2 = 120°, m3 = 120° 3. m3 = (50x + 20)°, m4= (100x – 80)° Alt. Int. s Thm.; m3 = 120°, m4 =120° 4. m3 = (45x + 30)°, m5 = (25x + 10)° Same-Side Int. s Thm.; m3 = 120°, m5 =6 ...
Angles Formed by Parallel Lines and Transversals
... 1. m1 = 120°, m2 = (60x)° Alt. Ext. s Thm.; m2 = 120° 2. m2 = (75x – 30)°, m3 = (30x + 60)° Corr. s Post.; m2 = 120°, m3 = 120° 3. m3 = (50x + 20)°, m4= (100x – 80)° Alt. Int. s Thm.; m3 = 120°, m4 =120° 4. m3 = (45x + 30)°, m5 = (25x + 10)° Same-Side Int. s Thm.; m3 = 120°, m5 =6 ...
... 1. m1 = 120°, m2 = (60x)° Alt. Ext. s Thm.; m2 = 120° 2. m2 = (75x – 30)°, m3 = (30x + 60)° Corr. s Post.; m2 = 120°, m3 = 120° 3. m3 = (50x + 20)°, m4= (100x – 80)° Alt. Int. s Thm.; m3 = 120°, m4 =120° 4. m3 = (45x + 30)°, m5 = (25x + 10)° Same-Side Int. s Thm.; m3 = 120°, m5 =6 ...