Read full issue - Canadian Mathematical Society
... Competition (see CRUX [20:65]) goes as follows: An isosceles triangle is called an amoeba if it can be divided into two isosceles triangles by a straight cut. How many di erent (that is, not similar) amoebas are there? All three authors wrote that contest. Afterwards, they felt that the problem woul ...
... Competition (see CRUX [20:65]) goes as follows: An isosceles triangle is called an amoeba if it can be divided into two isosceles triangles by a straight cut. How many di erent (that is, not similar) amoebas are there? All three authors wrote that contest. Afterwards, they felt that the problem woul ...
Ch. 4 Note Sheet L1 Name: A.Simons Page 1 of 18 Rigidity is a
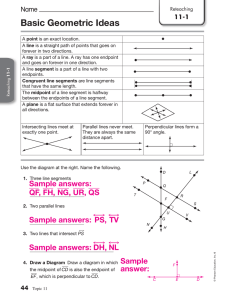
... deduce this information from definitions or conjectures that you already know to be true. Complete the following to help you review these statements. Remember, to mark your diagrams with the equal parts. Also never assume things are congruent! You must have a definitions or conjecture to back you up ...
... deduce this information from definitions or conjectures that you already know to be true. Complete the following to help you review these statements. Remember, to mark your diagrams with the equal parts. Also never assume things are congruent! You must have a definitions or conjecture to back you up ...
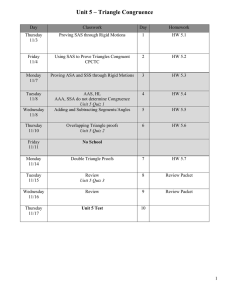
Problem Set #3
... Consider OB and a point A on one side of OB . The ray of the form OA can be matched one to one with real numbers from 0 to 180. The measure of AOB is equal to the absolute value of the difference between the real numbers for OA and OB . ...
... Consider OB and a point A on one side of OB . The ray of the form OA can be matched one to one with real numbers from 0 to 180. The measure of AOB is equal to the absolute value of the difference between the real numbers for OA and OB . ...
Constructions_2
... 1. Place compass at P and with distance PA set, draw arc at C. 2. With compass at A and distance set greater than AP, draw arc above line AB. 3. Repeat with compass at C and same distance set. 4. Draw line through intersection of arcs to P. This line is perpendicular to P. ...
... 1. Place compass at P and with distance PA set, draw arc at C. 2. With compass at A and distance set greater than AP, draw arc above line AB. 3. Repeat with compass at C and same distance set. 4. Draw line through intersection of arcs to P. This line is perpendicular to P. ...
3.1 The concept of parallelism
... began work on the fifth postulate in 1792 while only 15 years old, at first attempting to prove the parallels postulate from the other four. By 1813 he had made little progress and wrote: In the theory of parallels we are even now not further than Euclid. This is a shameful part of mathematics... Ho ...
... began work on the fifth postulate in 1792 while only 15 years old, at first attempting to prove the parallels postulate from the other four. By 1813 he had made little progress and wrote: In the theory of parallels we are even now not further than Euclid. This is a shameful part of mathematics... Ho ...