Chapter 7 PPT
... determined deviations on which the estimated standard deviation in the denominator of T is based. The use of t distribution in making inferences requires notation for capturing t-curve tail areas analogous to for the curve. You might think that t would do the trick. However, the desired value depen ...
... determined deviations on which the estimated standard deviation in the denominator of T is based. The use of t distribution in making inferences requires notation for capturing t-curve tail areas analogous to for the curve. You might think that t would do the trick. However, the desired value depen ...
How many times should you shuffle a deck of cards?
... this means. A permutation of X = {1, 2, . . . , n} is a one-to-one function π : X → X. Any two such functions, π1 , π2 , can be composed and the resulting function, π2 ◦π1 , is also a permutation. The inverse, π −1 , of a permutation is clearly also a permutation. The set of all permutations of X, w ...
... this means. A permutation of X = {1, 2, . . . , n} is a one-to-one function π : X → X. Any two such functions, π1 , π2 , can be composed and the resulting function, π2 ◦π1 , is also a permutation. The inverse, π −1 , of a permutation is clearly also a permutation. The set of all permutations of X, w ...
AP Statistics
... The knowledge acquired in AP Statistics is for the purpose of application. Nonetheless, before such knowledge may be applied, understanding must occur. Understanding is a measure of the number of cognitive connections that are made between the concepts of a topic or subject. Moreover, a higher level ...
... The knowledge acquired in AP Statistics is for the purpose of application. Nonetheless, before such knowledge may be applied, understanding must occur. Understanding is a measure of the number of cognitive connections that are made between the concepts of a topic or subject. Moreover, a higher level ...
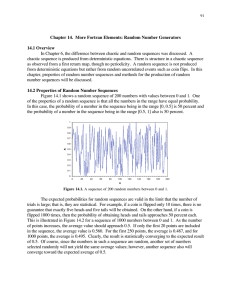
Chapter 14. More Fortran Elements: Random Number Generators
... sequences. That is, if the random number generator is given the same starting value (called the seed), then it will produce the same sequence every time. This behavior is known as a pseudorandom sequence, and it is useful for testing the Fortran code. The properties of a pseudo-random sequence are t ...
... sequences. That is, if the random number generator is given the same starting value (called the seed), then it will produce the same sequence every time. This behavior is known as a pseudorandom sequence, and it is useful for testing the Fortran code. The properties of a pseudo-random sequence are t ...
BINARY SEQUENCES WITHOUT ISOLATED ONES al = I 32 = 2, a
... Liu [2] asks for the number of sequences of zeros and ones of length five, such that every digit 1 has at least one neighboring 1. The solution [1] uses the principle of inclusion-exclusion, although it is easier in this particularcase to enumerate the twelve sequences: ...
... Liu [2] asks for the number of sequences of zeros and ones of length five, such that every digit 1 has at least one neighboring 1. The solution [1] uses the principle of inclusion-exclusion, although it is easier in this particularcase to enumerate the twelve sequences: ...
Risky strategies with payoff mean changed in 2×2 simulation
... The authors investigate the Nash equilibrium payoff in the 2×2 simulation-based game where the two strategic payoffs are Normal distribution and the equilibrium payoffs are realized after the decision-making. The researchers show that the risk premiums are a part of the means of equilibrium payoffs ...
... The authors investigate the Nash equilibrium payoff in the 2×2 simulation-based game where the two strategic payoffs are Normal distribution and the equilibrium payoffs are realized after the decision-making. The researchers show that the risk premiums are a part of the means of equilibrium payoffs ...
Central limit theorem

In probability theory, the central limit theorem (CLT) states that, given certain conditions, the arithmetic mean of a sufficiently large number of iterates of independent random variables, each with a well-defined expected value and well-defined variance, will be approximately normally distributed, regardless of the underlying distribution. That is, suppose that a sample is obtained containing a large number of observations, each observation being randomly generated in a way that does not depend on the values of the other observations, and that the arithmetic average of the observed values is computed. If this procedure is performed many times, the central limit theorem says that the computed values of the average will be distributed according to the normal distribution (commonly known as a ""bell curve"").The central limit theorem has a number of variants. In its common form, the random variables must be identically distributed. In variants, convergence of the mean to the normal distribution also occurs for non-identical distributions or for non-independent observations, given that they comply with certain conditions.In more general probability theory, a central limit theorem is any of a set of weak-convergence theorems. They all express the fact that a sum of many independent and identically distributed (i.i.d.) random variables, or alternatively, random variables with specific types of dependence, will tend to be distributed according to one of a small set of attractor distributions. When the variance of the i.i.d. variables is finite, the attractor distribution is the normal distribution. In contrast, the sum of a number of i.i.d. random variables with power law tail distributions decreasing as |x|−α−1 where 0 < α < 2 (and therefore having infinite variance) will tend to an alpha-stable distribution with stability parameter (or index of stability) of α as the number of variables grows.