Statistics
... each point: 2-4=-2, 2-4=-2, 4-4=0, 8-4=4 3. Square each difference:4,4,0,16 4. Add together: 4+4+0+16=24 5. Divide by #: 24 4 = 6 This is the variance 6. Take square root: 2.45 ...
... each point: 2-4=-2, 2-4=-2, 4-4=0, 8-4=4 3. Square each difference:4,4,0,16 4. Add together: 4+4+0+16=24 5. Divide by #: 24 4 = 6 This is the variance 6. Take square root: 2.45 ...
STAT 315: LECTURE 4 CHAPTER 4: CONTINUOUS RANDOM
... • A continuous random variable X is a rv that can take on any value within an interval, or union of disjoint intervals. – For a continuous rv X, the probability of any particular real number is zero, i.e. if X is a continuous rv, then P (X = x) = 0 for all x ∈ R. – For a continuous rv X, it only mak ...
... • A continuous random variable X is a rv that can take on any value within an interval, or union of disjoint intervals. – For a continuous rv X, the probability of any particular real number is zero, i.e. if X is a continuous rv, then P (X = x) = 0 for all x ∈ R. – For a continuous rv X, it only mak ...
Mean of a Discrete Random Variable - how-confident-ru
... Statistical estimation and the law of large numbers Law of large numbers Draw independent observations at random from any population with finite mean (μ). Decide how accurately you would like to estimate the mean. As the number of observations drawn increases, the mean of the observed values eventua ...
... Statistical estimation and the law of large numbers Law of large numbers Draw independent observations at random from any population with finite mean (μ). Decide how accurately you would like to estimate the mean. As the number of observations drawn increases, the mean of the observed values eventua ...
MA 1125 Lecture 12 - Mean and Standard Deviation for the Binomial
... This is a theoretical computation that applies to all conceivable repetitions of the experiment, so we’re doing a computation on a population. That means that we’re computing the parameter µ (the population mean). This is really a short cut to listing out one billion 0’s, three billion 1’s, three bi ...
... This is a theoretical computation that applies to all conceivable repetitions of the experiment, so we’re doing a computation on a population. That means that we’re computing the parameter µ (the population mean). This is really a short cut to listing out one billion 0’s, three billion 1’s, three bi ...
Midterm, Version 1
... 10) The Central Limit Theorem says that if we take a random sample of size n from an infinite population, then if n is sufficiently large A) The distribution of the values in the sample will be approximately normal B) The standard error of the sample mean will approach the standard deviation of the ...
... 10) The Central Limit Theorem says that if we take a random sample of size n from an infinite population, then if n is sufficiently large A) The distribution of the values in the sample will be approximately normal B) The standard error of the sample mean will approach the standard deviation of the ...
LAB1
... left scatterings. There are 14 rows of staggered pins. This is the n in the C.L.T. equation. Each scattering contributes a deviation, Yn, from the center horizontal location where the ball is released. The deviation can have positive or negative sign and its value depends on the particular angle of ...
... left scatterings. There are 14 rows of staggered pins. This is the n in the C.L.T. equation. Each scattering contributes a deviation, Yn, from the center horizontal location where the ball is released. The deviation can have positive or negative sign and its value depends on the particular angle of ...
Handout on Empirical Distribution Function
... The purpose of this handout is to show you how all of the common (univariate) descriptive statistics are computed and interpreted in terms of the so-called empirical distribution function. Suppose that we have a (univariate) dataset X1 , X2 , . . . , Xn consisting of observed values of random variab ...
... The purpose of this handout is to show you how all of the common (univariate) descriptive statistics are computed and interpreted in terms of the so-called empirical distribution function. Suppose that we have a (univariate) dataset X1 , X2 , . . . , Xn consisting of observed values of random variab ...
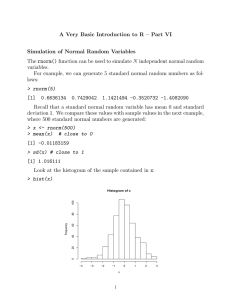
Simulation of Normal Random Numbers
... The rnorm() function can be used to simulate N independent normal random variables. For example, we can generate 5 standard normal random numbers as follows: > rnorm(5) ...
... The rnorm() function can be used to simulate N independent normal random variables. For example, we can generate 5 standard normal random numbers as follows: > rnorm(5) ...
The Poisson distribution The Poisson distribution is, like the
... probability which states that the sum of all probabilities in a given experiment must be 1. It follows that P[ X > 5] = 1 − P[ X ≤ 5] . Now, P[ X ≤ 5] = P[ X = 0] + P[ X = 1] + ....+ P[ X = 5] e −2 2 0 e −2 21 e −2 2 2 e −2 2 3 e −2 2 4 e −2 2 5 ...
... probability which states that the sum of all probabilities in a given experiment must be 1. It follows that P[ X > 5] = 1 − P[ X ≤ 5] . Now, P[ X ≤ 5] = P[ X = 0] + P[ X = 1] + ....+ P[ X = 5] e −2 2 0 e −2 21 e −2 2 2 e −2 2 3 e −2 2 4 e −2 2 5 ...
Probability—the description of random events
... e) X and s2 are themselves random variables. As such, they have their own means and variances (which can be calculated). 3. Expected value a) The expected value of a random variable X is written E(X). It is the value that one would obtain if a very large number of samples were averaged together. b) ...
... e) X and s2 are themselves random variables. As such, they have their own means and variances (which can be calculated). 3. Expected value a) The expected value of a random variable X is written E(X). It is the value that one would obtain if a very large number of samples were averaged together. b) ...
expected value - Ursinus College Student, Faculty and Staff Web
... Rules for Mean We have illustrated the principle that if X is random variable and Y is another random variable, then X+Y is also a random variable. We also have the formula μX+Y = μX+μY. Let a, b be fixed numbers. Another formula is μa+bX = a + bμX. This formula says that if I multiply or add a con ...
... Rules for Mean We have illustrated the principle that if X is random variable and Y is another random variable, then X+Y is also a random variable. We also have the formula μX+Y = μX+μY. Let a, b be fixed numbers. Another formula is μa+bX = a + bμX. This formula says that if I multiply or add a con ...
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Department of Civil and Environmental Engineering
... sample mean estimate is NOT the same as the variance of the data. d.) As the sample size increases, the confidence interval width decreases. This makes sense, since the more data points you have, the more confident you are in your estimate, so you can make your interval smaller, ie you are really su ...
... sample mean estimate is NOT the same as the variance of the data. d.) As the sample size increases, the confidence interval width decreases. This makes sense, since the more data points you have, the more confident you are in your estimate, so you can make your interval smaller, ie you are really su ...
Practice Exam 2 solutions
... favorite cereal. The four different prizes are randomly put into the boxes at the factory. If his mom decides to buy the cereal until all four prizes are obtained, then what is the expected number of boxes she will have to buy until the boy has obtained all four prizes? Solution: We can think of thi ...
... favorite cereal. The four different prizes are randomly put into the boxes at the factory. If his mom decides to buy the cereal until all four prizes are obtained, then what is the expected number of boxes she will have to buy until the boy has obtained all four prizes? Solution: We can think of thi ...
Random variable distributions
... Both the lognormal and Weibull distributions are used to model strength. Fit 100 data generated from a standard lognormal distribution by both lognormal and ...
... Both the lognormal and Weibull distributions are used to model strength. Fit 100 data generated from a standard lognormal distribution by both lognormal and ...
File
... should be close to the expected value, and will tend to become closer as more trials are performed. What does the proportion of heads begin to approach as the number of trials gets closer to ...
... should be close to the expected value, and will tend to become closer as more trials are performed. What does the proportion of heads begin to approach as the number of trials gets closer to ...
ST 3951 - Loyola College
... 8. If A and B are independent events, show that AC and BC are independent. 9. Show that E (X) = n P ( X n), for a random variable with values 0, 1, 2, 3... 10. Define partial correlation. SECTION - B Answer any FIVE questions. ...
... 8. If A and B are independent events, show that AC and BC are independent. 9. Show that E (X) = n P ( X n), for a random variable with values 0, 1, 2, 3... 10. Define partial correlation. SECTION - B Answer any FIVE questions. ...