MATH3303: 2015 FINAL EXAM (1) Show that Z/mZ × Z/nZ is cyclic if
... (1) Show that Z/mZ × Z/nZ is cyclic if and only if gcd(m, n) = 1. Solution. The group in question consists of mn elements: G := Z/mZ × Z/nZ = {(a, b) : a ∈ Z/mZ, b ∈ Z/nZ} and is equipped with the multiplication (a, b) · (c, d) = (ac, bd). Clearly, G has order mn. The element (a, b) ∈ G will be a ge ...
... (1) Show that Z/mZ × Z/nZ is cyclic if and only if gcd(m, n) = 1. Solution. The group in question consists of mn elements: G := Z/mZ × Z/nZ = {(a, b) : a ∈ Z/mZ, b ∈ Z/nZ} and is equipped with the multiplication (a, b) · (c, d) = (ac, bd). Clearly, G has order mn. The element (a, b) ∈ G will be a ge ...
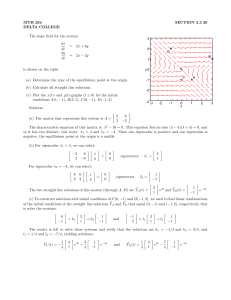
MTH 264 SECTION 3.3 20 DELTA COLLEGE The slope field for the
... The characteristic equation of this matrix is: λ2 − 16 = 0. This equation factors into (λ − 4)(λ + 4) = 0, and so it has two distinct, real roots: λ1 = 4 and λ2 = −4. Since one eigenvalue is positive and one eigenvalue is negative, the equilibrium point at the origin is a saddle. (b) For eigenvalue ...
... The characteristic equation of this matrix is: λ2 − 16 = 0. This equation factors into (λ − 4)(λ + 4) = 0, and so it has two distinct, real roots: λ1 = 4 and λ2 = −4. Since one eigenvalue is positive and one eigenvalue is negative, the equilibrium point at the origin is a saddle. (b) For eigenvalue ...
Print test
... 1) The second number is 3 more than the first number. 2) The product of the two numbers is 9 more than their sum. Which of the following represents possible values of these two numbers? ...
... 1) The second number is 3 more than the first number. 2) The product of the two numbers is 9 more than their sum. Which of the following represents possible values of these two numbers? ...
Linear Systems Gaussian Elimination
... A given equation can be multiplied by a non-zero constant and the result substituted for the original equation, A given equation can be added to a second equation, and the result substituted for the original equation, Two equations can be transposed in order. ...
... A given equation can be multiplied by a non-zero constant and the result substituted for the original equation, A given equation can be added to a second equation, and the result substituted for the original equation, Two equations can be transposed in order. ...
More Lecture Notes in Algebra 1 (Fall Semester 2013)
... matrices but different right hand sides can be solved simultaneously with the same augmented matrix: one just writes the different right hand sides next to each other. Determine a and b so that the lines y − 3x = 2 and 2y + ax = b a) intersect at a point, b) are parallel and different, c) coincide. ...
... matrices but different right hand sides can be solved simultaneously with the same augmented matrix: one just writes the different right hand sides next to each other. Determine a and b so that the lines y − 3x = 2 and 2y + ax = b a) intersect at a point, b) are parallel and different, c) coincide. ...
Linear Transformations and Matrices
... (or small group of firsts) then from this first you can create another (or others) then more and more by applying a rule to get another element in the set are our focus here. If all elements (members) are in the set because they are either the first (basis) or can be constructed by applying ”The” ru ...
... (or small group of firsts) then from this first you can create another (or others) then more and more by applying a rule to get another element in the set are our focus here. If all elements (members) are in the set because they are either the first (basis) or can be constructed by applying ”The” ru ...
Ch 4-1 Intro to Matrices
... 4 columns Answer: Since matrix G has 2 rows and 4 columns, the dimensions of matrix G are 2 4. ...
... 4 columns Answer: Since matrix G has 2 rows and 4 columns, the dimensions of matrix G are 2 4. ...
Linear algebra
Linear algebra is the branch of mathematics concerning vector spaces and linear mappings between such spaces. It includes the study of lines, planes, and subspaces, but is also concerned with properties common to all vector spaces.The set of points with coordinates that satisfy a linear equation forms a hyperplane in an n-dimensional space. The conditions under which a set of n hyperplanes intersect in a single point is an important focus of study in linear algebra. Such an investigation is initially motivated by a system of linear equations containing several unknowns. Such equations are naturally represented using the formalism of matrices and vectors.Linear algebra is central to both pure and applied mathematics. For instance, abstract algebra arises by relaxing the axioms of a vector space, leading to a number of generalizations. Functional analysis studies the infinite-dimensional version of the theory of vector spaces. Combined with calculus, linear algebra facilitates the solution of linear systems of differential equations.Techniques from linear algebra are also used in analytic geometry, engineering, physics, natural sciences, computer science, computer animation, and the social sciences (particularly in economics). Because linear algebra is such a well-developed theory, nonlinear mathematical models are sometimes approximated by linear models.