PATH CONNECTEDNESS AND INVERTIBLE MATRICES 1. Path
... answers to these related questions requires more sophisticated background knowledge, so keep that in mind while reading this section. 4.1. Invertible Matrices over R. In the previous section, we considered matrices with complex entries. What happens when we consider invertible matrices with real ent ...
... answers to these related questions requires more sophisticated background knowledge, so keep that in mind while reading this section. 4.1. Invertible Matrices over R. In the previous section, we considered matrices with complex entries. What happens when we consider invertible matrices with real ent ...
Some definitions that may be useful
... Tannaka-Krein theory asks two main questions: (Reconstruction) What about an algebraic object can you determine based on knowledge about its representation theory? (Recognition) Which alleged ”representation theories” actually arise as the representation theories of algebraic objects? In this talk I ...
... Tannaka-Krein theory asks two main questions: (Reconstruction) What about an algebraic object can you determine based on knowledge about its representation theory? (Recognition) Which alleged ”representation theories” actually arise as the representation theories of algebraic objects? In this talk I ...
BOOLEAN ALGEBRA Boolean algebra, or the algebra of logic, was
... "multiplication") and "–" (called Boolean complementation: note that the operation sending x, y to x i (–y) corresponds to Boole's "subtraction") are known as Boolean operations. The elements 0 and 1 are called the zero and unit elements of B, respectively. A Boolean algebra is customarily identifie ...
... "multiplication") and "–" (called Boolean complementation: note that the operation sending x, y to x i (–y) corresponds to Boole's "subtraction") are known as Boolean operations. The elements 0 and 1 are called the zero and unit elements of B, respectively. A Boolean algebra is customarily identifie ...
A simple proof of Valiant`s lemma
... triangular matrix. The crucial point of his approach is to design this procedure even in the case, where the product opération is non-associative. His algorithm uses several propositions on dividing a matrix into certain submatrices to obtain the transitive closure by recursiveness. One of these pro ...
... triangular matrix. The crucial point of his approach is to design this procedure even in the case, where the product opération is non-associative. His algorithm uses several propositions on dividing a matrix into certain submatrices to obtain the transitive closure by recursiveness. One of these pro ...
MATLab Tutorial #6
... When using the term-by-term multiplication, the vectors/matrices being multiplied must be the same size, since corresponding terms are multiplied. This is not what we typically think of as matrix multiplication. If we were to do a regular multiplication of these two vectors: >> x * y ??? Error usin ...
... When using the term-by-term multiplication, the vectors/matrices being multiplied must be the same size, since corresponding terms are multiplied. This is not what we typically think of as matrix multiplication. If we were to do a regular multiplication of these two vectors: >> x * y ??? Error usin ...
Two-dimensional space-time symmetry in hyperbolic functions
... It is interesting to note that the same result is normally achieved by following a number of “formal” steps [10, p.94], [11, p.50], i.e. by introducing an “imaginary” time t′ = it which makes the Lorentz invariant (x2 − t2 ) equivalent to the rotation invariant (x2 + y 2 ), and by introducing the hy ...
... It is interesting to note that the same result is normally achieved by following a number of “formal” steps [10, p.94], [11, p.50], i.e. by introducing an “imaginary” time t′ = it which makes the Lorentz invariant (x2 − t2 ) equivalent to the rotation invariant (x2 + y 2 ), and by introducing the hy ...
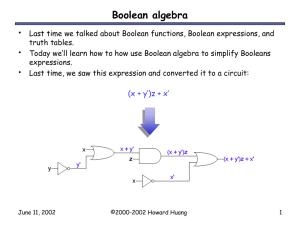
Boolean Algebra
... Here are the circuits resulting from the original and simplified expressions on the previous page. ...
... Here are the circuits resulting from the original and simplified expressions on the previous page. ...
Lyapunov Operator Let A ∈ F n×n be given, and define a linear
... Recall that for any square matrix M, there is a “largest” stable invariant subspace. That is, there is a stable invariant subspace VS∗ that contains every other stable invariant subspace of M. This largest stable invariant subspace is simply the span of all of the eigenvectors and generalized eigenv ...
... Recall that for any square matrix M, there is a “largest” stable invariant subspace. That is, there is a stable invariant subspace VS∗ that contains every other stable invariant subspace of M. This largest stable invariant subspace is simply the span of all of the eigenvectors and generalized eigenv ...
Linear algebra
Linear algebra is the branch of mathematics concerning vector spaces and linear mappings between such spaces. It includes the study of lines, planes, and subspaces, but is also concerned with properties common to all vector spaces.The set of points with coordinates that satisfy a linear equation forms a hyperplane in an n-dimensional space. The conditions under which a set of n hyperplanes intersect in a single point is an important focus of study in linear algebra. Such an investigation is initially motivated by a system of linear equations containing several unknowns. Such equations are naturally represented using the formalism of matrices and vectors.Linear algebra is central to both pure and applied mathematics. For instance, abstract algebra arises by relaxing the axioms of a vector space, leading to a number of generalizations. Functional analysis studies the infinite-dimensional version of the theory of vector spaces. Combined with calculus, linear algebra facilitates the solution of linear systems of differential equations.Techniques from linear algebra are also used in analytic geometry, engineering, physics, natural sciences, computer science, computer animation, and the social sciences (particularly in economics). Because linear algebra is such a well-developed theory, nonlinear mathematical models are sometimes approximated by linear models.