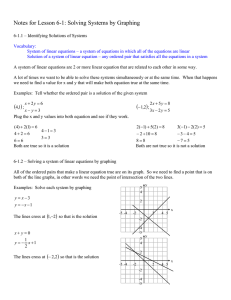
Defn: A set V together with two operations, called addition and
... Defn: A set V together with two operations, called addition and scalar multiplication is a vector space if the following vector space axioms are satisfied for all vectors u, v, and w in V and all scalars, c, d in R. Vector space axioms: a.) u + v is in V b.) cu is in V c.) u + v = v + u d.) (u + v) ...
... Defn: A set V together with two operations, called addition and scalar multiplication is a vector space if the following vector space axioms are satisfied for all vectors u, v, and w in V and all scalars, c, d in R. Vector space axioms: a.) u + v is in V b.) cu is in V c.) u + v = v + u d.) (u + v) ...
Classification of linear transformations from R2 to R2 In mathematics
... Classification of linear transformations from R2 to R2 In mathematics, one way we “understand” mathematical objects is to classify them (when we can). For this, we have some definition of the objects as being isomorphic (essentially the same), and then understand when two objects are isomorphic. If ...
... Classification of linear transformations from R2 to R2 In mathematics, one way we “understand” mathematical objects is to classify them (when we can). For this, we have some definition of the objects as being isomorphic (essentially the same), and then understand when two objects are isomorphic. If ...
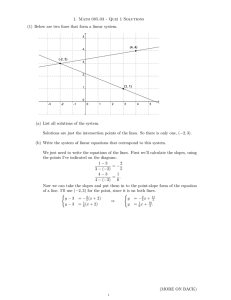
Math 362 Practice Exam I 1. Find the Cartesian and polar form of the
... (a) Multiply matrices A and B to get AB. (b) Does BA exist? Justify your answer. (c) Are the columns of matrix A linearly independent? Justify your answer. (d) Find the rank of A, B, and AB. (e) Do the columns of matrix A span R3? Justify your answer. (f) Do the columns of matrix B span R2? Justify ...
... (a) Multiply matrices A and B to get AB. (b) Does BA exist? Justify your answer. (c) Are the columns of matrix A linearly independent? Justify your answer. (d) Find the rank of A, B, and AB. (e) Do the columns of matrix A span R3? Justify your answer. (f) Do the columns of matrix B span R2? Justify ...
Definitions in Problem 1 of Exam Review
... 1. Complete each of the following to provide proper definitions or complete, general descriptions. Operational definitions (i.e. descriptions of how the object is calculated ) will receive at most half credit. Note that there are many equivalent ways to express the definitions of these terms. Mathem ...
... 1. Complete each of the following to provide proper definitions or complete, general descriptions. Operational definitions (i.e. descriptions of how the object is calculated ) will receive at most half credit. Note that there are many equivalent ways to express the definitions of these terms. Mathem ...
Homework2-F14-LinearAlgebra.pdf
... [9] Let V be the vector space of all polynomials of degree 6 2 in the variable x with coefficients in R. Let W be the subspace consisting of those polynomials f(x) such that f(−1) = 0. Find the orthogonal projection of the polynomial x + 1 onto the subspace W , with respect to the inner product ...
... [9] Let V be the vector space of all polynomials of degree 6 2 in the variable x with coefficients in R. Let W be the subspace consisting of those polynomials f(x) such that f(−1) = 0. Find the orthogonal projection of the polynomial x + 1 onto the subspace W , with respect to the inner product ...
Exam2-1010-S13-LinearAlgebra.pdf
... [2] By least squares, find the equation of the form y = ax + b which best fits the data (x1 , y1 ) = (0, 1), ...
... [2] By least squares, find the equation of the form y = ax + b which best fits the data (x1 , y1 ) = (0, 1), ...
Sections 1.8 and 1.9
... algebra (and applications) in a way that is not directly connected with linear combinations of vectors. ...
... algebra (and applications) in a way that is not directly connected with linear combinations of vectors. ...
Linear algebra
Linear algebra is the branch of mathematics concerning vector spaces and linear mappings between such spaces. It includes the study of lines, planes, and subspaces, but is also concerned with properties common to all vector spaces.The set of points with coordinates that satisfy a linear equation forms a hyperplane in an n-dimensional space. The conditions under which a set of n hyperplanes intersect in a single point is an important focus of study in linear algebra. Such an investigation is initially motivated by a system of linear equations containing several unknowns. Such equations are naturally represented using the formalism of matrices and vectors.Linear algebra is central to both pure and applied mathematics. For instance, abstract algebra arises by relaxing the axioms of a vector space, leading to a number of generalizations. Functional analysis studies the infinite-dimensional version of the theory of vector spaces. Combined with calculus, linear algebra facilitates the solution of linear systems of differential equations.Techniques from linear algebra are also used in analytic geometry, engineering, physics, natural sciences, computer science, computer animation, and the social sciences (particularly in economics). Because linear algebra is such a well-developed theory, nonlinear mathematical models are sometimes approximated by linear models.