The Inertia Tensor and After Dinner Tricks
... the shortest vector which points from the axis of rotation to the volume element. Actually when we discuss a “force” which changes the way an object rotates we call it a torque rather than a force. The variable I will use for torque is N. Just as when there are no forces acting on an object momentum ...
... the shortest vector which points from the axis of rotation to the volume element. Actually when we discuss a “force” which changes the way an object rotates we call it a torque rather than a force. The variable I will use for torque is N. Just as when there are no forces acting on an object momentum ...
14 Conservation of Energy - DigitalCommons@USU
... After all of these developments it is nice to keep in mind the idea that the wave equation describes (a continuum limit of) a network of coupled oscillators. This raises an interesting question. Certainly you have seen by now how important energy and momentum — and their conservation — are for under ...
... After all of these developments it is nice to keep in mind the idea that the wave equation describes (a continuum limit of) a network of coupled oscillators. This raises an interesting question. Certainly you have seen by now how important energy and momentum — and their conservation — are for under ...
AP Physics C Rotational Physics Free Response Problems A very
... 5. A block A of mass M is suspended from a light string that passes over a pulley and is connected to block B of mass 2M. Block B sits on the surface of a smooth table. Block C of mass 3M sits on the top of block B. The surface between block C and block B is not frictionless. When the system of thr ...
... 5. A block A of mass M is suspended from a light string that passes over a pulley and is connected to block B of mass 2M. Block B sits on the surface of a smooth table. Block C of mass 3M sits on the top of block B. The surface between block C and block B is not frictionless. When the system of thr ...
view as pdf - KITP Online
... For classical (x) the exact equation for the fermion D(x,y) reads: ...
... For classical (x) the exact equation for the fermion D(x,y) reads: ...
July 2010
... A first problem they would face is that the universe may be infinitely large and contain an infinite amount of matter and energy. Thus, the accountants would need to take a shortcut. They would draw an imaginary membrane around a region of the universe and add up the energy inside [see box on page 3 ...
... A first problem they would face is that the universe may be infinitely large and contain an infinite amount of matter and energy. Thus, the accountants would need to take a shortcut. They would draw an imaginary membrane around a region of the universe and add up the energy inside [see box on page 3 ...
Ch 8.3 - 8.5 chap 8.3
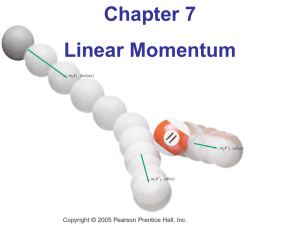
... Chap 8.3 and 8.4 Conservation of Momentum •Conservation of Linear Momentum • Inelastic Collisions • Elastic Collisions ...
... Chap 8.3 and 8.4 Conservation of Momentum •Conservation of Linear Momentum • Inelastic Collisions • Elastic Collisions ...
無投影片標題
... – B3 = 0 , once a particle enters in region III, there is no potential changes to cause a reflection, therefore, B3 must be zero. – At x = 0 and x = a, the corresponding wave function and its first ...
... – B3 = 0 , once a particle enters in region III, there is no potential changes to cause a reflection, therefore, B3 must be zero. – At x = 0 and x = a, the corresponding wave function and its first ...
Notes on Elementary Particle Physics
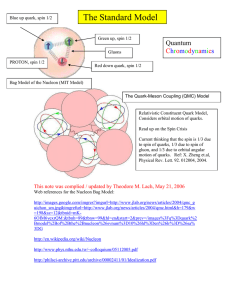
... The electromagnetic binding enegy for a proton-antiproton (pp) system is about 14 keV, however the binding energy for a deuteron (np) is about 2 MeV. So the residual strong force is about 100 times stronger than the electromagnetic force. In the same way the strong force is around 100 to 1000 times ...
... The electromagnetic binding enegy for a proton-antiproton (pp) system is about 14 keV, however the binding energy for a deuteron (np) is about 2 MeV. So the residual strong force is about 100 times stronger than the electromagnetic force. In the same way the strong force is around 100 to 1000 times ...
Laser-dressed scattering of an attosecond electron wave
... In this paper, we theoretically study how a laser field affects the scattering of an attosecond electron wave packet as it travels inside a spatially extended system. Experimentally, this can be realized by ionizing a localized electronic state of a molecule with an attosecond extreme-ultraviolet (X ...
... In this paper, we theoretically study how a laser field affects the scattering of an attosecond electron wave packet as it travels inside a spatially extended system. Experimentally, this can be realized by ionizing a localized electronic state of a molecule with an attosecond extreme-ultraviolet (X ...