Chemistry 102 Summary June 25th - Bohr model only works for one
... For a very massive ball, the wavelength is so short that we cannot detect the wave motion (basically moves in a straight line). For very small particles like electrons, the wave properties are extremely important when discussing overall characteristics. The movement of electrons about the nucleus ca ...
... For a very massive ball, the wavelength is so short that we cannot detect the wave motion (basically moves in a straight line). For very small particles like electrons, the wave properties are extremely important when discussing overall characteristics. The movement of electrons about the nucleus ca ...
Quantum Algorithms for Neural Networks Daniel Shumow
... at once. This is called a super position of states. • Quantum systems are described by a wave function often denoted by the Greek letter (psi) • For state x: (x) evaluates to a complex number such that (x)·(x)* is the probability that the quantum system will collapse into state x when it intera ...
... at once. This is called a super position of states. • Quantum systems are described by a wave function often denoted by the Greek letter (psi) • For state x: (x) evaluates to a complex number such that (x)·(x)* is the probability that the quantum system will collapse into state x when it intera ...
Spacetime structures of continuous
... for our understanding of physics. In quantum mechanics, next to the harmonic oscillator, the particle in a box provides much insight into the quantum world 共e.g. 关1兴兲. Recently, the problem of a quantum mechanical particle initially characterized by a Gaussian wave packet and moving in an infinite b ...
... for our understanding of physics. In quantum mechanics, next to the harmonic oscillator, the particle in a box provides much insight into the quantum world 共e.g. 关1兴兲. Recently, the problem of a quantum mechanical particle initially characterized by a Gaussian wave packet and moving in an infinite b ...
Condensed matter
... In 1979 the first confined gas of bosons, spinpolarized atomic hydrogen was stabilized, but the conditions for BEC were difficult to achieve. In the 1980s atomic physicists learned how to cool alkali atoms (sodium, rubidium,etc.) to microkelvin temperatures Alkali gases (metastable) were confined i ...
... In 1979 the first confined gas of bosons, spinpolarized atomic hydrogen was stabilized, but the conditions for BEC were difficult to achieve. In the 1980s atomic physicists learned how to cool alkali atoms (sodium, rubidium,etc.) to microkelvin temperatures Alkali gases (metastable) were confined i ...
Electromagnetic Radiation
... The Aufbau Principles and the Periodic Table Periodic Trends in Atomic Properties The Properties of a Group: The Alkali Metals ...
... The Aufbau Principles and the Periodic Table Periodic Trends in Atomic Properties The Properties of a Group: The Alkali Metals ...
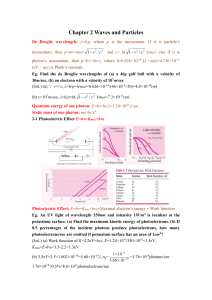
Chapter 2 Waves and Particles De Broglie wavelength: λ=h/p, where
... light whose original frequency is 7.3×1014Hz when it fall through 22.5m. (Sol.) H=22.5, △ν=gHν/c2=1.8Hz ...
... light whose original frequency is 7.3×1014Hz when it fall through 22.5m. (Sol.) H=22.5, △ν=gHν/c2=1.8Hz ...
Atomic Structure and Atomic Spectra
... Since a photon carries energy and angular momentum (1 unit), any electronic transition from one allowed energy level to another must conserve energy and angular momentum for the atom-photon system. Thus, restrictions on the allowed changes in multiplicity, orbital and total angular momentum can be p ...
... Since a photon carries energy and angular momentum (1 unit), any electronic transition from one allowed energy level to another must conserve energy and angular momentum for the atom-photon system. Thus, restrictions on the allowed changes in multiplicity, orbital and total angular momentum can be p ...
Hypercomputation - the UNC Department of Computer Science
... In quantum mechanics, the wave-particle duality is explained as follows: every system and particle is described by wave functions which encode the probability distributions of all measurable variables. The position of the particle is one such variable. Before an observation is made the position of t ...
... In quantum mechanics, the wave-particle duality is explained as follows: every system and particle is described by wave functions which encode the probability distributions of all measurable variables. The position of the particle is one such variable. Before an observation is made the position of t ...
NATURAL UNITS AND PLANE WAVES Natural Units A.1
... It is common and useful to use natural units in derivations and problem solving. This serves to save time and make the equations more transparent by eliminating the physical constants which tend to clutter the equations. In contrast to the popular belief, once you have developed the knack of placing ...
... It is common and useful to use natural units in derivations and problem solving. This serves to save time and make the equations more transparent by eliminating the physical constants which tend to clutter the equations. In contrast to the popular belief, once you have developed the knack of placing ...
Particle in a box

In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example a ball trapped inside a large box, the particle can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow (on the scale of a few nanometers), quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never ""sit still"". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.The particle in a box model provides one of the very few problems in quantum mechanics which can be solved analytically, without approximations. This means that the observable properties of the particle (such as its energy and position) are related to the mass of the particle and the width of the well by simple mathematical expressions. Due to its simplicity, the model allows insight into quantum effects without the need for complicated mathematics. It is one of the first quantum mechanics problems taught in undergraduate physics courses, and it is commonly used as an approximation for more complicated quantum systems.