Name 8-1 Notes IB Math SL Lesson 8
... A probability distribution/probability model is a table/chart that displays _________________________ along with their _____________________ __________________. A probability model has two parts: 1) A list of _______________________________________________ and 2) The probability that _______________ ...
... A probability distribution/probability model is a table/chart that displays _________________________ along with their _____________________ __________________. A probability model has two parts: 1) A list of _______________________________________________ and 2) The probability that _______________ ...
Binomial random variables
... 3. The probability is 0.04 that a person reached on a “cold call” by a telemarketer will make a purchase. If the telemarketer calls 40 people, what is the probability that at least one sale with ...
... 3. The probability is 0.04 that a person reached on a “cold call” by a telemarketer will make a purchase. If the telemarketer calls 40 people, what is the probability that at least one sale with ...
K.K. Gan Physics 416 Problem Set 2 Due Thursday, October 28, 2004
... 6) Suppose a missile defense system destroys an incoming missile 95% of the time. a) If an evil country launches 20 missiles what is the probability that the missile defense system will destroy all of the incoming missiles? b) How many missiles have to be launched to have a 50% chance of at least on ...
... 6) Suppose a missile defense system destroys an incoming missile 95% of the time. a) If an evil country launches 20 missiles what is the probability that the missile defense system will destroy all of the incoming missiles? b) How many missiles have to be launched to have a 50% chance of at least on ...
Section 4.3 Homework Answers
... days. Call the length of a randomly chosen pregnancy Y. (a) Make a sketch of the density curve for this random variable. ...
... days. Call the length of a randomly chosen pregnancy Y. (a) Make a sketch of the density curve for this random variable. ...
Document
... Ex: Baby gender. The probability of having a boy is 50%. My sister-in-law just had a girl (and is expecting another!). The probability works when applied to the whole population (large number of trials), not when applied to my sister-in-law (a single experiment). ...
... Ex: Baby gender. The probability of having a boy is 50%. My sister-in-law just had a girl (and is expecting another!). The probability works when applied to the whole population (large number of trials), not when applied to my sister-in-law (a single experiment). ...
Sect 12.5 Adding Probabilities
... Try another one … 1) Peyton has a stack of 8 baseball cards, 5 basketball cards, and 6 soccer cards. If she selects a card at random from the stack, what is the probability that it is a baseball or a soccer card? ...
... Try another one … 1) Peyton has a stack of 8 baseball cards, 5 basketball cards, and 6 soccer cards. If she selects a card at random from the stack, what is the probability that it is a baseball or a soccer card? ...
10.1 Introduction to Probability
... The overall likelihood, or probability, of an event can be discovered by observing the results of a large number of repetitions of the situation in which the event may occur. Outcomes are random if all possible outcomes are equally likely. I. The terminology used to discuss probabilities is given b ...
... The overall likelihood, or probability, of an event can be discovered by observing the results of a large number of repetitions of the situation in which the event may occur. Outcomes are random if all possible outcomes are equally likely. I. The terminology used to discuss probabilities is given b ...
BIN0406-15 Introduction to probability and statistics (4-0-4)
... BIN0406-15 Introduction to probability and statistics (4-0-4) General goals: The main goal of this course is to introduce the essential concepts of the theory of probability, such as probability spaces, random variables, distribution functions, etc., together with its implications and applications i ...
... BIN0406-15 Introduction to probability and statistics (4-0-4) General goals: The main goal of this course is to introduce the essential concepts of the theory of probability, such as probability spaces, random variables, distribution functions, etc., together with its implications and applications i ...
The Power of Probability - The Actuarial Foundation
... 7.SP.2. Use data from a random sample to draw inferences about a population with an unknown characteristic of interest. Generate multiple samples (or simulated samples) of the same size to gauge the variation in estimates or predictions. For example, estimate the mean word length in a book by random ...
... 7.SP.2. Use data from a random sample to draw inferences about a population with an unknown characteristic of interest. Generate multiple samples (or simulated samples) of the same size to gauge the variation in estimates or predictions. For example, estimate the mean word length in a book by random ...
104Peterson/exII
... "heads", whichever comes first. Let X count the number of flips in a trial. What is the expected value of the random variable X? ...
... "heads", whichever comes first. Let X count the number of flips in a trial. What is the expected value of the random variable X? ...
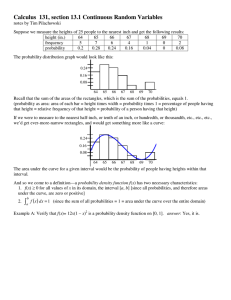
Calculus 131, section 13.1 Continuous Random Variables
... And so we come to a definition—a probability density function f(x) has two necessary characteristics: 1. f(x) ≥ 0 for all values of x in its domain, the interval [a, b] [since all probabilities, and therefore areas under the curve, are zero or positive] ...
... And so we come to a definition—a probability density function f(x) has two necessary characteristics: 1. f(x) ≥ 0 for all values of x in its domain, the interval [a, b] [since all probabilities, and therefore areas under the curve, are zero or positive] ...
Probability Density Functions A continuous random variable takes
... A continuous random variable takes on an uncountably infinite number of possible values. For a discrete random variable X that takes on a finite or countably infinite number of possible values, we determined P(X = x) for all of the possible values of X, and called it the probability mass function (" ...
... A continuous random variable takes on an uncountably infinite number of possible values. For a discrete random variable X that takes on a finite or countably infinite number of possible values, we determined P(X = x) for all of the possible values of X, and called it the probability mass function (" ...
Ars Conjectandi

Ars Conjectandi (Latin for The Art of Conjecturing) is a book on combinatorics and mathematical probability written by Jakob Bernoulli and published in 1713, eight years after his death, by his nephew, Niklaus Bernoulli. The seminal work consolidated, apart from many combinatorial topics, many central ideas in probability theory, such as the very first version of the law of large numbers: indeed, it is widely regarded as the founding work of that subject. It also addressed problems that today are classified in the twelvefold way, and added to the subjects; consequently, it has been dubbed an important historical landmark in not only probability but all combinatorics by a plethora of mathematical historians. The importance of this early work had a large impact on both contemporary and later mathematicians; for example, Abraham de Moivre.Bernoulli wrote the text between 1684 and 1689, including the work of mathematicians such as Christiaan Huygens, Gerolamo Cardano, Pierre de Fermat, and Blaise Pascal. He incorporated fundamental combinatorial topics such as his theory of permutations and combinations—the aforementioned problems from the twelvefold way—as well as those more distantly connected to the burgeoning subject: the derivation and properties of the eponymous Bernoulli numbers, for instance. Core topics from probability, such as expected value, were also a significant portion of this important work.