Physical Probability 2 Physical Probability as a
... and H is the coin landing heads, qX 2 (HH) = [qX (H)]2 . ...
... and H is the coin landing heads, qX 2 (HH) = [qX (H)]2 . ...
Unit 1 Review Part 1
... 2. You roll a number cube numbered from 1 to 6. You then spin a spinner with 5 sections each with a different color. The spinner has the colors red, pink, orange, green, and navy. P(2 and red) 3. If one letter is chosen at random from the word refuse, what is the probability that the letter chosen i ...
... 2. You roll a number cube numbered from 1 to 6. You then spin a spinner with 5 sections each with a different color. The spinner has the colors red, pink, orange, green, and navy. P(2 and red) 3. If one letter is chosen at random from the word refuse, what is the probability that the letter chosen i ...
Unit 1 Review Part 1
... 2. You roll a number cube numbered from 1 to 6. You then spin a spinner with 5 sections each with a different color. The spinner has the colors red, pink, orange, green, and navy. P(2 and red) 3. If one letter is chosen at random from the word refuse, what is the probability that the letter chosen i ...
... 2. You roll a number cube numbered from 1 to 6. You then spin a spinner with 5 sections each with a different color. The spinner has the colors red, pink, orange, green, and navy. P(2 and red) 3. If one letter is chosen at random from the word refuse, what is the probability that the letter chosen i ...
5 - Web4students
... ENTER (this is one repetition of the experiment) Repeat the experiment 25 times and record information in the table. (keep pressing ENTER 24 more times and tally results below) #head s ...
... ENTER (this is one repetition of the experiment) Repeat the experiment 25 times and record information in the table. (keep pressing ENTER 24 more times and tally results below) #head s ...
Intro to Probability
... person portray the recessive trait. When a parent has both a dominant and a recessive gene, then the two genes are equally likely to be passed to a child. Immunity to poison ivy is a dominant trait. Suppose that a child has two parents who both have just one dominant poison ivy immunity gene. What i ...
... person portray the recessive trait. When a parent has both a dominant and a recessive gene, then the two genes are equally likely to be passed to a child. Immunity to poison ivy is a dominant trait. Suppose that a child has two parents who both have just one dominant poison ivy immunity gene. What i ...
p.p chapter 5.2
... collection of outcomes and their probabilities. • This is what’s known as an Event- any collection of outcomes from some chance process. Events are assigned capital letters such as A,B,C • P(A) where A= sum of 5. ...
... collection of outcomes and their probabilities. • This is what’s known as an Event- any collection of outcomes from some chance process. Events are assigned capital letters such as A,B,C • P(A) where A= sum of 5. ...
this will live in learning village
... Any probability answers will come from recorded data or information from an experiment. ...
... Any probability answers will come from recorded data or information from an experiment. ...
Form groups of two or three and discuss the following questions
... Note that the solution will be discussed in full during Session 11. (iii) After being born alive into this population, can you work out what the probability is of surviving from birth to exact age 5? Note that the solution should be clearer after Session 3. 4. You will meet mortality rate schedules ...
... Note that the solution will be discussed in full during Session 11. (iii) After being born alive into this population, can you work out what the probability is of surviving from birth to exact age 5? Note that the solution should be clearer after Session 3. 4. You will meet mortality rate schedules ...
Subject: Math 3 Grade: 10-12 Unit #: 1 Title: Probability UNIT
... Estimate the answer to any probability problem that arises. ...
... Estimate the answer to any probability problem that arises. ...
Document
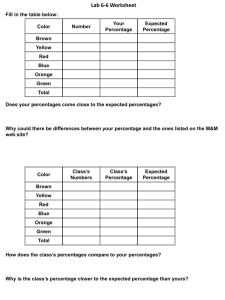
... Suppose you had placed all the M&M’s form the class experiment into a jar. If one candy is randomly selected, what is the probability that you will select a red M&M? ...
... Suppose you had placed all the M&M’s form the class experiment into a jar. If one candy is randomly selected, what is the probability that you will select a red M&M? ...
PS Ch. 3.3 Notes (completed)
... Event A: Randomly select a blood donor with type O blood. Event B: Randomly select a female blood donor. ...
... Event A: Randomly select a blood donor with type O blood. Event B: Randomly select a female blood donor. ...
Sec. 3.3 – The Addition Rule
... Event A: Randomly select a blood donor with type O blood. Event B: Randomly select a female blood donor. ...
... Event A: Randomly select a blood donor with type O blood. Event B: Randomly select a female blood donor. ...
Ars Conjectandi

Ars Conjectandi (Latin for The Art of Conjecturing) is a book on combinatorics and mathematical probability written by Jakob Bernoulli and published in 1713, eight years after his death, by his nephew, Niklaus Bernoulli. The seminal work consolidated, apart from many combinatorial topics, many central ideas in probability theory, such as the very first version of the law of large numbers: indeed, it is widely regarded as the founding work of that subject. It also addressed problems that today are classified in the twelvefold way, and added to the subjects; consequently, it has been dubbed an important historical landmark in not only probability but all combinatorics by a plethora of mathematical historians. The importance of this early work had a large impact on both contemporary and later mathematicians; for example, Abraham de Moivre.Bernoulli wrote the text between 1684 and 1689, including the work of mathematicians such as Christiaan Huygens, Gerolamo Cardano, Pierre de Fermat, and Blaise Pascal. He incorporated fundamental combinatorial topics such as his theory of permutations and combinations—the aforementioned problems from the twelvefold way—as well as those more distantly connected to the burgeoning subject: the derivation and properties of the eponymous Bernoulli numbers, for instance. Core topics from probability, such as expected value, were also a significant portion of this important work.