notes
... 4. Unsymmetric eigenvalue problems (Ch 7) 5. Symmetric eigenvalue problems (Ch 8) 6. Iterative methods (Ch 10–11) We could also organize the course by four over-arching themes: 1. Algebra: matrix factorizations and such 2. Analysis: perturbation theory, convergence, error analysis, etc. 3. Algorithm ...
... 4. Unsymmetric eigenvalue problems (Ch 7) 5. Symmetric eigenvalue problems (Ch 8) 6. Iterative methods (Ch 10–11) We could also organize the course by four over-arching themes: 1. Algebra: matrix factorizations and such 2. Analysis: perturbation theory, convergence, error analysis, etc. 3. Algorithm ...
Sections 3.4-3.6
... A vector space so large that no finite set of vectors spans it is called infinitedimensional. The Dimension of the Column Space of a Matrix Column Space of a Matrix: The pivot columns of a matrix A form a basis for ColA. Then the dimension of the column space, denoted dim(ColA), is the number of pi ...
... A vector space so large that no finite set of vectors spans it is called infinitedimensional. The Dimension of the Column Space of a Matrix Column Space of a Matrix: The pivot columns of a matrix A form a basis for ColA. Then the dimension of the column space, denoted dim(ColA), is the number of pi ...
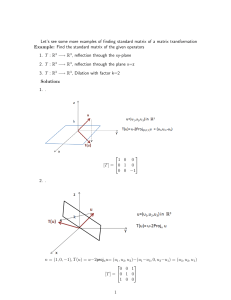
Find the standard matrix of the gi
... To be able to define inverse of a matrix transformation we need to have one-to-one matrix operator Definition: A matrix transformation T : Rn → Rm is said to be one-to-one if T maps distinct vectors (points) in Rn into distinct vectors (points) in Rm . That is for each w in the range of T, there is ...
... To be able to define inverse of a matrix transformation we need to have one-to-one matrix operator Definition: A matrix transformation T : Rn → Rm is said to be one-to-one if T maps distinct vectors (points) in Rn into distinct vectors (points) in Rm . That is for each w in the range of T, there is ...