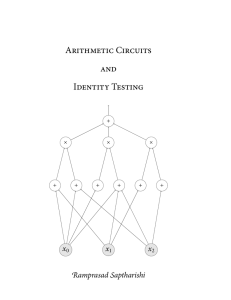
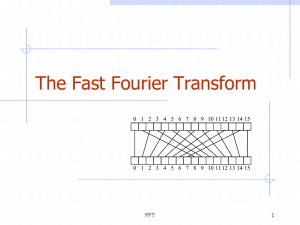
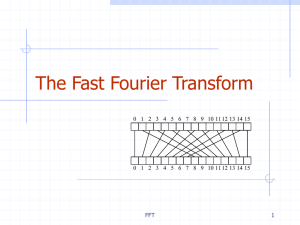
Lie Groups and Algebraic Groups
... n × n identity matrix by I (or In if the size of the matrix needs to be indicated); it has entries δij = 1 if i = j and 0 otherwise. Let V be an n-dimensional vector space / V is a linear map we write µ(T ) over F with basis {v1 , . . . , vn }. If T : V for the matrix of T with respect to this basis ...
... n × n identity matrix by I (or In if the size of the matrix needs to be indicated); it has entries δij = 1 if i = j and 0 otherwise. Let V be an n-dimensional vector space / V is a linear map we write µ(T ) over F with basis {v1 , . . . , vn }. If T : V for the matrix of T with respect to this basis ...
Galois Field Computations A Galois field is an algebraic field that
... how to work with fields that have 2m members, where m is an integer between 1 and 16. Such fields are denoted GF(2m). Galois fields having 2m members are used in error-control coding. If you need to use Galois fields having an odd number of elements, see Appendix: Galois Fields of Odd Characteristic ...
... how to work with fields that have 2m members, where m is an integer between 1 and 16. Such fields are denoted GF(2m). Galois fields having 2m members are used in error-control coding. If you need to use Galois fields having an odd number of elements, see Appendix: Galois Fields of Odd Characteristic ...
Introduction to tensor, tensor factorization and its applications
... Apply CP to reconstruct a MATLAB logo from noisy data ...
... Apply CP to reconstruct a MATLAB logo from noisy data ...