Synopsis of Geometric Algebra
... Although the vector space Vn is closed under vector addition, it is not closed under multiplication, as the contraction rule (1.3) shows. Instead, by multiplication and addition the vectors of Vn generate a larger linear space Gn = G(Vn ) called the geometric algebra of Vn . This linear space is, of ...
... Although the vector space Vn is closed under vector addition, it is not closed under multiplication, as the contraction rule (1.3) shows. Instead, by multiplication and addition the vectors of Vn generate a larger linear space Gn = G(Vn ) called the geometric algebra of Vn . This linear space is, of ...
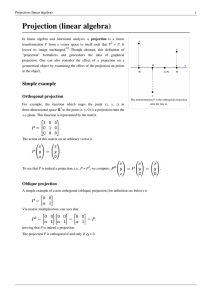
Projection (linear algebra)
... questions, irrelevant in the finite-dimensional case, need to be considered. Assume now X is a Banach space. Many of the algebraic notions discussed above survive the passage to this context. A given direct sum decomposition of X into complementary subspaces still specifies a projection, and vice ve ...
... questions, irrelevant in the finite-dimensional case, need to be considered. Assume now X is a Banach space. Many of the algebraic notions discussed above survive the passage to this context. A given direct sum decomposition of X into complementary subspaces still specifies a projection, and vice ve ...