Chapter 5 Part 1 Solving Inequalities File
... Here are the assignments that you are expected to complete for this unit. Each assignment will be scored based on correct answers and showing your work. Correct answers are worth 1 point and correctly showing your work is worth 2 points. Therefor each assignment is worth a total of 3 points. The las ...
... Here are the assignments that you are expected to complete for this unit. Each assignment will be scored based on correct answers and showing your work. Correct answers are worth 1 point and correctly showing your work is worth 2 points. Therefor each assignment is worth a total of 3 points. The las ...
Sample Final - University of Nebraska–Lincoln
... 6. Consider the linear congruence equation ax ≡ b (mod 36). (a) Construct a linear congruence equation modulo 36 with no solutions. (b) Construct a linear congruence equation modulo 36 with exactly 1 solution. (c) Construct a linear congruence equation modulo 36 with more than one solution. 7. Solve ...
... 6. Consider the linear congruence equation ax ≡ b (mod 36). (a) Construct a linear congruence equation modulo 36 with no solutions. (b) Construct a linear congruence equation modulo 36 with exactly 1 solution. (c) Construct a linear congruence equation modulo 36 with more than one solution. 7. Solve ...
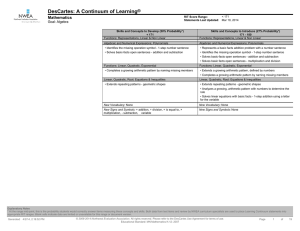
Definition
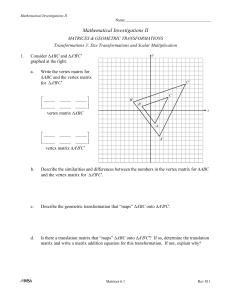
... A1AB = A1C (NOT AA1B = CA1!) You must multiply matrix A by its inverse A 1 on the left hand side of A ( not right hand side! ) But A 1A = I hence we can simplify to IB = A1C B = A1C ...
... A1AB = A1C (NOT AA1B = CA1!) You must multiply matrix A by its inverse A 1 on the left hand side of A ( not right hand side! ) But A 1A = I hence we can simplify to IB = A1C B = A1C ...