Ch - Cobb Learning
... Name _______________________________________ Date __________________ Class __________________ ...
... Name _______________________________________ Date __________________ Class __________________ ...
Name ____________________________________________ Date ___________ Color _______ Algebra I Ms. Hahl
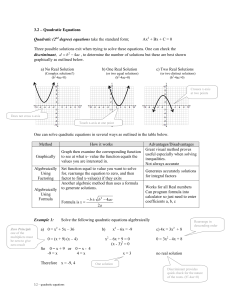
... Solving absolute value equations is almost the exact same as solving regular equations with one major difference. In most cases you have 2 solutions. Example: |x|=5 We know that when x = 5, | 5 | will also equal 5, but it is also true that | -5 | will equal 5. So, for |x | = 5, x = {-5, 5}. They bot ...
... Solving absolute value equations is almost the exact same as solving regular equations with one major difference. In most cases you have 2 solutions. Example: |x|=5 We know that when x = 5, | 5 | will also equal 5, but it is also true that | -5 | will equal 5. So, for |x | = 5, x = {-5, 5}. They bot ...
Solving and Graphing Linear Equations in Two Variables
... Solving and Graphing Linear Equations in Two Variables-Answer Key Across 4. Linear ...
... Solving and Graphing Linear Equations in Two Variables-Answer Key Across 4. Linear ...
Section 2.5 Solving Equations with variables on both sides
... and/or subtraction to get all the variables on one side of the equation and the constant terms on the other side. ...
... and/or subtraction to get all the variables on one side of the equation and the constant terms on the other side. ...
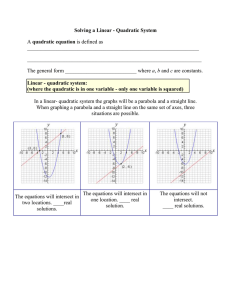
Systems of Equations
... STEPS for ADDITION or SUBTRACTION ELIMINATION: 1) Add or subtract the equations in order to cancel one of the variables. (It all depends on the coefficients and signs of each variable.) 2) Solve the resulting equation for the variable. 3) Use that answer to find the other variable by substituting it ...
... STEPS for ADDITION or SUBTRACTION ELIMINATION: 1) Add or subtract the equations in order to cancel one of the variables. (It all depends on the coefficients and signs of each variable.) 2) Solve the resulting equation for the variable. 3) Use that answer to find the other variable by substituting it ...
Here
... solutions to the system A? Solution: The vector w is in the span of these vectors. We can see this by solving the system of linear equations A. The first equation is equivalent to x1 = 1 + 3x3 which, substituted into the second equation, yields x2 = 1 + 3x3 + 2(1 + 3x3 ) = 3 + 9x3 If we choose x3 = ...
... solutions to the system A? Solution: The vector w is in the span of these vectors. We can see this by solving the system of linear equations A. The first equation is equivalent to x1 = 1 + 3x3 which, substituted into the second equation, yields x2 = 1 + 3x3 + 2(1 + 3x3 ) = 3 + 9x3 If we choose x3 = ...