vectors
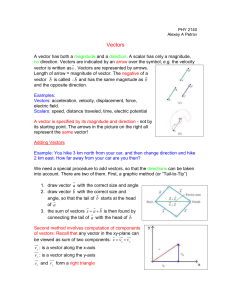
... Scalars: speed, distance traveled, time, electric potential A vector is specified by its magnitude and direction - not by its starting point. The arrows in the picture on the right all represent the same vector! Adding Vectors Example: You hike 3 km north from your car, and then change direction and ...
... Scalars: speed, distance traveled, time, electric potential A vector is specified by its magnitude and direction - not by its starting point. The arrows in the picture on the right all represent the same vector! Adding Vectors Example: You hike 3 km north from your car, and then change direction and ...
Geometric algebra
A geometric algebra (GA) is a Clifford algebra of a vector space over the field of real numbers endowed with a quadratic form. The term is also sometimes used as a collective term for the approach to classical, computational and relativistic geometry that applies these algebras. The Clifford multiplication that defines the GA as a unital ring is called the geometric product. Taking the geometric product among vectors can yield bivectors, trivectors, or general n-vectors. The addition operation combines these into general multivectors, which are the elements of the ring. This includes, among other possibilities, a well-defined formal sum of a scalar and a vector.Geometric algebra is distinguished from Clifford algebra in general by its restriction to real numbers and its emphasis on its geometric interpretation and physical applications. Specific examples of geometric algebras applied in physics include the algebra of physical space, the spacetime algebra, and the conformal geometric algebra. Geometric calculus, an extension of GA that incorporates differentiation and integration can be used to formulate other theories such as complex analysis, differential geometry, e.g. by using the Clifford algebra instead of differential forms. Geometric algebra has been advocated, most notably by David Hestenes and Chris Doran, as the preferred mathematical framework for physics. Proponents claim that it provides compact and intuitive descriptions in many areas including classical and quantum mechanics, electromagnetic theory and relativity. GA has also found use as a computational tool in computer graphics and robotics.The geometric product was first briefly mentioned by Hermann Grassmann, who was chiefly interested in developing the closely related exterior algebra, which is the geometric algebra of the trivial quadratic form. In 1878, William Kingdon Clifford greatly expanded on Grassmann's work to form what are now usually called Clifford algebras in his honor (although Clifford himself chose to call them ""geometric algebras""). For several decades, geometric algebras went somewhat ignored, greatly eclipsed by the vector calculus then newly developed to describe electromagnetism. The term ""geometric algebra"" was repopularized by Hestenes in the 1960s, who recognized its importance to relativistic physics.