Carom 1-16 - s253053503.websitehome.co.uk
... Let us call π(x) the number of primes less than x. So π(20) = 8. If we were to draw a graph of π(x) against x, what would it look like? We can tell roughly from our work above that it will look roughly like this: ...
... Let us call π(x) the number of primes less than x. So π(20) = 8. If we were to draw a graph of π(x) against x, what would it look like? We can tell roughly from our work above that it will look roughly like this: ...
NUMBER FRACTION AND RELATED FUNCTIONS
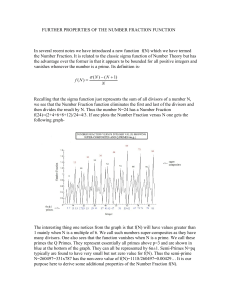
... Here σ(N) is the sigma function( also known as the divisor function) representing the sum of all divisors of N. Thus N=36 has σ(36)= 91 and f(36)=3/2. What is important about the f(N) function is that it vanishes whenever N is a prime and seems to be bounded to less than about 5 for all N (This conj ...
... Here σ(N) is the sigma function( also known as the divisor function) representing the sum of all divisors of N. Thus N=36 has σ(36)= 91 and f(36)=3/2. What is important about the f(N) function is that it vanishes whenever N is a prime and seems to be bounded to less than about 5 for all N (This conj ...
Arbitrarily Large Gaps Between Primes - PSU Math Home
... and the last divisible by 5. So here we have four consecutive non‐primes, meaning that we have a gap of at least four (4) between two consecutive primes. Three comments are in order related to this result and the proof above. 1) Notice how this proof “borrows from” Eucl ...
... and the last divisible by 5. So here we have four consecutive non‐primes, meaning that we have a gap of at least four (4) between two consecutive primes. Three comments are in order related to this result and the proof above. 1) Notice how this proof “borrows from” Eucl ...
THE E.IRREGULAR PRIMES
... primes is infinite. The proof is similar to the corresponding proof mentioned above. one might therefore expect that it would also be easy to obtain results on the distribution of .E-irregular primes, by modifying suitable methods used in connection with the ordinary irregular primes. It seems, howe ...
... primes is infinite. The proof is similar to the corresponding proof mentioned above. one might therefore expect that it would also be easy to obtain results on the distribution of .E-irregular primes, by modifying suitable methods used in connection with the ordinary irregular primes. It seems, howe ...
Greatest common divisor as a product of primes
... Clive Newstead, 18th March 2014 The Fundamental Theorem of Arithmetic (FTA) is all about products of primes: it tells you that every natural number greater than 1 has a representation as a product of primes, and moreover that expression is unique up to reordering. We can use this to find an expressi ...
... Clive Newstead, 18th March 2014 The Fundamental Theorem of Arithmetic (FTA) is all about products of primes: it tells you that every natural number greater than 1 has a representation as a product of primes, and moreover that expression is unique up to reordering. We can use this to find an expressi ...