Structure and Randomness in the Prime Numbers
... Theorem 1 (Euclid’s Theorem). There are infinitely many primes. In particular, given any k, there exists a prime with at least k digits. But there is no known quick and deterministic way to locate such a prime! (Here, “quick” means “computable in a time which is polynomial in k”.) In particular, ther ...
... Theorem 1 (Euclid’s Theorem). There are infinitely many primes. In particular, given any k, there exists a prime with at least k digits. But there is no known quick and deterministic way to locate such a prime! (Here, “quick” means “computable in a time which is polynomial in k”.) In particular, ther ...
PDF
... For all other positive integers the value of Carmichael’s function is the least common multiple of all the dividing primes raised to the appropriate powers (e.g., to calculate ψ(504) we’d reckon ψ(23 ), ψ(32 ) and ψ(7) and find the LCM of these). Sequence A002322 in Sloane’s OEIS gives values of ψ(n ...
... For all other positive integers the value of Carmichael’s function is the least common multiple of all the dividing primes raised to the appropriate powers (e.g., to calculate ψ(504) we’d reckon ψ(23 ), ψ(32 ) and ψ(7) and find the LCM of these). Sequence A002322 in Sloane’s OEIS gives values of ψ(n ...
Full text
... function of the primes, the ftth prime p , the function i\(x) , and the least prime greater than a given number. These formulas are all elementary functions in the sense of Grzegorczyk [6] and Kalmar [12] (Kalmar elementary). From a theorem of Jones [11], it will follow that there exist formulas wit ...
... function of the primes, the ftth prime p , the function i\(x) , and the least prime greater than a given number. These formulas are all elementary functions in the sense of Grzegorczyk [6] and Kalmar [12] (Kalmar elementary). From a theorem of Jones [11], it will follow that there exist formulas wit ...
Perfect Numbers - University of Arizona Math
... called Mersenne primes. A Mersenne prime is a prime number that can be written as 2p - 1, where p is some other prime number. For example, when p = 2, then 22 - 1 = 4 - 1 = 3, so 3 is a Mersenne prime. Every perfect number that has been discovered so far has a Mersenne prime as one of its factors. C ...
... called Mersenne primes. A Mersenne prime is a prime number that can be written as 2p - 1, where p is some other prime number. For example, when p = 2, then 22 - 1 = 4 - 1 = 3, so 3 is a Mersenne prime. Every perfect number that has been discovered so far has a Mersenne prime as one of its factors. C ...
6.00 Introduction to Computer Science and Programming
... 1. Initialize some state variables 2. Generate all (odd) integers > 1 as candidates to be prime 3. For each candidate integer, test whether it is prime 1. One easy way to do this is to test whether any other integer > 1 evenly divides the candidate with 0 remainder. To do this, you can use modular a ...
... 1. Initialize some state variables 2. Generate all (odd) integers > 1 as candidates to be prime 3. For each candidate integer, test whether it is prime 1. One easy way to do this is to test whether any other integer > 1 evenly divides the candidate with 0 remainder. To do this, you can use modular a ...
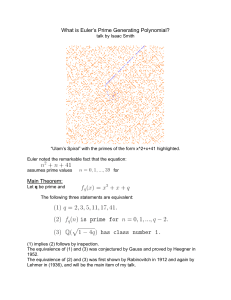
What is Euler`s Prime Generating Polynomial? Main Theorem:
... Lehmer in (1936), and will be the main item of my talk. ...
... Lehmer in (1936), and will be the main item of my talk. ...