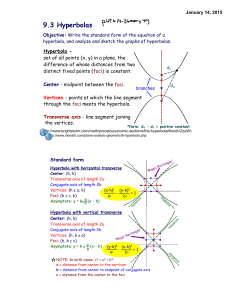
Coordinate Geometry
... greater than but not equal to –3 . A closed circle would have indicated that x is greater than or equal to –3 . For the solution set –3 < x < 3 , where x must be greater than –3 and less than 3 , the line graph looks like this: ...
... greater than but not equal to –3 . A closed circle would have indicated that x is greater than or equal to –3 . For the solution set –3 < x < 3 , where x must be greater than –3 and less than 3 , the line graph looks like this: ...
Mathematical Billiards
... Suppose P0 and P1 are points on a path P0, P1, P2, P3,…Pn in an ellipse and a focus point lies on the line segment P0P1 (see Figure 12). Then the points P0, P2, P4,… converge to one vertex and the points P1, P3, P5,… converge to the other vertex. The vertices on an ellipse are the left most point an ...
... Suppose P0 and P1 are points on a path P0, P1, P2, P3,…Pn in an ellipse and a focus point lies on the line segment P0P1 (see Figure 12). Then the points P0, P2, P4,… converge to one vertex and the points P1, P3, P5,… converge to the other vertex. The vertices on an ellipse are the left most point an ...
classwork geometry 5/13/2012
... as a conic cross-section, similar to parabola and ellipse. Namely, hyperbola is the curve of intersection between a right circular conical surface and a plane that cuts through both halves of the cone. For the other major types of conic sections, the ellipse and the parabola, the plane cuts through ...
... as a conic cross-section, similar to parabola and ellipse. Namely, hyperbola is the curve of intersection between a right circular conical surface and a plane that cuts through both halves of the cone. For the other major types of conic sections, the ellipse and the parabola, the plane cuts through ...
On Kepler`s First Law
... known (via [PI] and [P2]); and with the focus being given, together with a point P on the curve, the tangent to the curve at P and the curvature of the curve at P, a unique conic section C may be described. The two curves 0 and C now coincide at P upto curvature, a second degree quantity. The fact t ...
... known (via [PI] and [P2]); and with the focus being given, together with a point P on the curve, the tangent to the curve at P and the curvature of the curve at P, a unique conic section C may be described. The two curves 0 and C now coincide at P upto curvature, a second degree quantity. The fact t ...
Lecture 25
... between the two scores was not given but is known to be quite high. If you can estimate this correlation as, say, .7, you can find the equation of the regression line and use it to estimate the math score from a student’s verbal score. ...
... between the two scores was not given but is known to be quite high. If you can estimate this correlation as, say, .7, you can find the equation of the regression line and use it to estimate the math score from a student’s verbal score. ...
Tangents to Curves
... Lines and Circles • Given any two distinct points, we can use our straightedge to draw a unique straight line that passes through both of the points • Given any fixed point in the plane, and any fixed distance, we can use our compass to draw a unique circle having the point as its center and the di ...
... Lines and Circles • Given any two distinct points, we can use our straightedge to draw a unique straight line that passes through both of the points • Given any fixed point in the plane, and any fixed distance, we can use our compass to draw a unique circle having the point as its center and the di ...
PDF
... Basic concepts 1. incidence, 2. betweenness, 3. congruence, 4. similarity, 5. continuity, 6. parallelism, 7. perpendicularity, 8. corresponding angles in transversal cutting 9. intercept theorem 10. locus 11. dilation and translation, 12. rotation and reflection, 13. inversion of plane, 14. harmoni ...
... Basic concepts 1. incidence, 2. betweenness, 3. congruence, 4. similarity, 5. continuity, 6. parallelism, 7. perpendicularity, 8. corresponding angles in transversal cutting 9. intercept theorem 10. locus 11. dilation and translation, 12. rotation and reflection, 13. inversion of plane, 14. harmoni ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... 13. Separate tanh (x + iy) into real and imaginary parts. 1 cos i sin 14. Find the value of Log ...
... 13. Separate tanh (x + iy) into real and imaginary parts. 1 cos i sin 14. Find the value of Log ...
Ellipse
In mathematics, an ellipse is a curve on a plane surrounding two focal points such that the sum of the distances to the two focal points is constant for every point on the curve. As such, it is a generalization of a circle, which is a special type of an ellipse that has both focal points at the same location. The shape of an ellipse (how 'elongated' it is) is represented by its eccentricity, which for an ellipse can be any number from 0 (the limiting case of a circle) to arbitrarily close to but less than 1.Ellipses are the closed type of conic section: a plane curve that results from the intersection of a cone by a plane. (See figure to the right.) Ellipses have many similarities with the other two forms of conic sections: the parabolas and the hyperbolas, both of which are open and unbounded. The cross section of a cylinder is an ellipse, unless the section is parallel to the axis of the cylinder.Analytically, an ellipse can also be defined as the set of points such that the ratio of the distance of each point on the curve from a given point (called a focus or focal point) to the distance from that same point on the curve to a given line (called the directrix) is a constant, called the eccentricity of the ellipse.Ellipses are common in physics, astronomy and engineering. For example, the orbit of each planet in the solar system is an ellipse with the barycenter of the planet-Sun pair at one of the focal points. The same is true for moons orbiting planets and all other systems having two astronomical bodies. The shape of planets and stars are often well described by ellipsoids. Ellipses also arise as images of a circle under parallel projection and the bounded cases of perspective projection, which are simply intersections of the projective cone with the plane of projection. It is also the simplest Lissajous figure, formed when the horizontal and vertical motions are sinusoids with the same frequency. A similar effect leads to elliptical polarization of light in optics.The name, ἔλλειψις (élleipsis, ""omission""), was given by Apollonius of Perga in his Conics, emphasizing the connection of the curve with ""application of areas"".