4 Ideals in commutative rings
... Proof. Say a1 , . . . , an is a finite set of elements which generates hU i. Each aj is in thePideal generated by T and hence can be written in the form (a finite sum) i rij tij sij for some elements rij , sij ∈ R and tij ∈ T . Then the ideal hV i generated by the finite subset V = {tij }ij of T con ...
... Proof. Say a1 , . . . , an is a finite set of elements which generates hU i. Each aj is in thePideal generated by T and hence can be written in the form (a finite sum) i rij tij sij for some elements rij , sij ∈ R and tij ∈ T . Then the ideal hV i generated by the finite subset V = {tij }ij of T con ...
Direct-sum decompositions over local rings
... for all v ∈ C. Using linear independence of {1, a1 , b1 } we see that µ = 0, σ = ρ, and σν1 = ν1 ρ. Thus σ commutes with the non-derogatory matrix ν1 and therefore belongs to F[ν1 ]. Since φ is by assumption idempotent, it follows from (2.2.5) that σ is idempotent as well, and since F[ν1 ] is local, ...
... for all v ∈ C. Using linear independence of {1, a1 , b1 } we see that µ = 0, σ = ρ, and σν1 = ν1 ρ. Thus σ commutes with the non-derogatory matrix ν1 and therefore belongs to F[ν1 ]. Since φ is by assumption idempotent, it follows from (2.2.5) that σ is idempotent as well, and since F[ν1 ] is local, ...
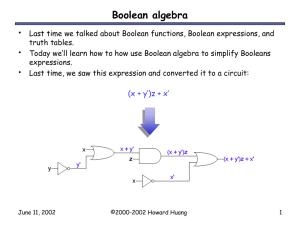
Boolean Algebra
... The operations we chose do satisfy all of the axioms. We can show this by looking at the definitions of our operations. x ...
... The operations we chose do satisfy all of the axioms. We can show this by looking at the definitions of our operations. x ...
Brauer groups of abelian schemes
... si an isomorphism. Since the left hand vertical map of (1.1) is monic, the map between these functors evaluated at S is a monomorphism and so is an isomorphism which proves the first part of (1). The diagram analogous to (1.1) derived from the Kummer sequence with n < oo replaces Q//Z/ with Z/^ Z. A ...
... si an isomorphism. Since the left hand vertical map of (1.1) is monic, the map between these functors evaluated at S is a monomorphism and so is an isomorphism which proves the first part of (1). The diagram analogous to (1.1) derived from the Kummer sequence with n < oo replaces Q//Z/ with Z/^ Z. A ...
Bertini irreducibility theorems over finite fields
... Let X be a geometrically irreducible variety of dimension m ≥ 2 over a field k. Let F be a finite set of closed points in X . Then there exists a geometrically irreducible variety of dimension m − 1 Y ⊂ X containing F . Used in a similar form by Duncan-Reichstein, as well as Panin, who raised the qu ...
... Let X be a geometrically irreducible variety of dimension m ≥ 2 over a field k. Let F be a finite set of closed points in X . Then there exists a geometrically irreducible variety of dimension m − 1 Y ⊂ X containing F . Used in a similar form by Duncan-Reichstein, as well as Panin, who raised the qu ...
8. Cyclotomic polynomials - Math-UMN
... On the other hand, for the harder half of the assertion, suppose P e−1 divides both f and Df . Write f /P e−1 = Q · P + R with deg R < deg P . Then f = QP e + RP e−1 . Differentiating, Df = DQ P e + eQP e−1 DP + DR P e−1 + R(e − 1)P e−2 DP By hypothesis P e−1 divides Df . All terms on the right-hand ...
... On the other hand, for the harder half of the assertion, suppose P e−1 divides both f and Df . Write f /P e−1 = Q · P + R with deg R < deg P . Then f = QP e + RP e−1 . Differentiating, Df = DQ P e + eQP e−1 DP + DR P e−1 + R(e − 1)P e−2 DP By hypothesis P e−1 divides Df . All terms on the right-hand ...
Lecture 2 - Stony Brook Mathematics
... Since Z/nZ is a ring for any n ≥ 1, it suffices to check that for n = p a prime that each 0 6= x ∈ Z/pZ has a multiplicative inverse. Choose the representative for the class x with 0 < x < p. Since p does not divide x, GCD(x, p) = 1, and thus, by the Euclidean algorithm, there exists b, y ∈ Z such t ...
... Since Z/nZ is a ring for any n ≥ 1, it suffices to check that for n = p a prime that each 0 6= x ∈ Z/pZ has a multiplicative inverse. Choose the representative for the class x with 0 < x < p. Since p does not divide x, GCD(x, p) = 1, and thus, by the Euclidean algorithm, there exists b, y ∈ Z such t ...
Existence of almost Cohen-Macaulay algebras implies the existence
... A big Cohen-Macaulay algebra over a local ring (R, m) is an R-algebra B such that some system of parameters of R is a regular sequence on B. It is balanced if every system of parameters of R is a regular sequence on B. Big Cohen-Macaulay algebras exist in equal characteristic [7], [6] and also in mi ...
... A big Cohen-Macaulay algebra over a local ring (R, m) is an R-algebra B such that some system of parameters of R is a regular sequence on B. It is balanced if every system of parameters of R is a regular sequence on B. Big Cohen-Macaulay algebras exist in equal characteristic [7], [6] and also in mi ...
Finite-model theory - a personal perspective *
... exclusively with finite-model theory. I was disappointed that the field languished for years afterwards: very few papers were published in the area in the next ten years or so. However, in the mid-1970s Hajek [55, 561 discussed the importance of finite model theory. In fact, in [56], Hajek made the ...
... exclusively with finite-model theory. I was disappointed that the field languished for years afterwards: very few papers were published in the area in the next ten years or so. However, in the mid-1970s Hajek [55, 561 discussed the importance of finite model theory. In fact, in [56], Hajek made the ...
Categories - University of Oregon
... There are some logical problems with the foundations of category theory. So we’re going to need some basic notions of set theory, about which I want to be as vague as possible. In set theory, there are two basic notions: the notion of a class and the notion of ‘is an element of’, ∈. It’s best not to ...
... There are some logical problems with the foundations of category theory. So we’re going to need some basic notions of set theory, about which I want to be as vague as possible. In set theory, there are two basic notions: the notion of a class and the notion of ‘is an element of’, ∈. It’s best not to ...
Notes - Mathematics and Statistics
... Note that though in a certain sense F and G are inverses, G is not uniquely determined by F ; its definition very much depends on the choice of maps ηA . 2.3.3. A criterion for equivalence. There is a general criteria for a functor F to be a natural equivalence of categories. The proof is not harder ...
... Note that though in a certain sense F and G are inverses, G is not uniquely determined by F ; its definition very much depends on the choice of maps ηA . 2.3.3. A criterion for equivalence. There is a general criteria for a functor F to be a natural equivalence of categories. The proof is not harder ...
Third symmetric power L-functions for GL(2)
... Proof of Theorem 4.1 is based on mixing the properties of RankinSelberg L-functions for GL2 x GL3 applied to 03C0 x n (Theorem 4.2) and those of Eisenstein series on a group of type G2. Here n is the adjoint square lift of 03C0 (cf. Sections 1 and 4; also see [3]). There is a second set of results i ...
... Proof of Theorem 4.1 is based on mixing the properties of RankinSelberg L-functions for GL2 x GL3 applied to 03C0 x n (Theorem 4.2) and those of Eisenstein series on a group of type G2. Here n is the adjoint square lift of 03C0 (cf. Sections 1 and 4; also see [3]). There is a second set of results i ...
Birkhoff's representation theorem
This is about lattice theory. For other similarly named results, see Birkhoff's theorem (disambiguation).In mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets. The theorem can be interpreted as providing a one-to-one correspondence between distributive lattices and partial orders, between quasi-ordinal knowledge spaces and preorders, or between finite topological spaces and preorders. It is named after Garrett Birkhoff, who published a proof of it in 1937.The name “Birkhoff's representation theorem” has also been applied to two other results of Birkhoff, one from 1935 on the representation of Boolean algebras as families of sets closed under union, intersection, and complement (so-called fields of sets, closely related to the rings of sets used by Birkhoff to represent distributive lattices), and Birkhoff's HSP theorem representing algebras as products of irreducible algebras. Birkhoff's representation theorem has also been called the fundamental theorem for finite distributive lattices.