Rigid Body Dynamics
... So far we have formulated classical mechanics in inertial frames of reference, i.e., those vector bases in which Newton’s second law holds (we have also allowed general coordinates, in which the Euler-Lagrange equations hold). However, it is sometimes useful to use non-inertial frames, and particula ...
... So far we have formulated classical mechanics in inertial frames of reference, i.e., those vector bases in which Newton’s second law holds (we have also allowed general coordinates, in which the Euler-Lagrange equations hold). However, it is sometimes useful to use non-inertial frames, and particula ...
Chapter 14
... In this equation, k is the spring constant, which depends on the stiffness and other properties of the spring, and x is the distance that the spring is stretched from its equilibrium position. Not all springs obey Hooke’s law, but many do. Those that do are called elastic. Potential energy When a fo ...
... In this equation, k is the spring constant, which depends on the stiffness and other properties of the spring, and x is the distance that the spring is stretched from its equilibrium position. Not all springs obey Hooke’s law, but many do. Those that do are called elastic. Potential energy When a fo ...
Momentum, Kinetic Energy and Arrow Penetration
... direction. Because any measurement of momentum has a specified direction it quantifies the net force acting in that single, straight line, direction. Momentum is, therefore, known as a linear function, and is a measurement of the force of forward movement of an object. Nerd's Note: While there are s ...
... direction. Because any measurement of momentum has a specified direction it quantifies the net force acting in that single, straight line, direction. Momentum is, therefore, known as a linear function, and is a measurement of the force of forward movement of an object. Nerd's Note: While there are s ...
pdf file
... is addressed in a case study on potentialities for (loco)motion in physics, with specific reference to how a potentiality for ‘quantity of motion’ and one for ‘moving force’ were developed in classical mechanics as developed by Descartes, Huygens, Newton and Leibniz, among others—known as ‘momentum’ ...
... is addressed in a case study on potentialities for (loco)motion in physics, with specific reference to how a potentiality for ‘quantity of motion’ and one for ‘moving force’ were developed in classical mechanics as developed by Descartes, Huygens, Newton and Leibniz, among others—known as ‘momentum’ ...
Chapter 7: Linear Momentum and Collisions
... into a duck pond. Two 4.0-kg ducks and a 7.6-kg goose paddle rapidly toward the bread from opposite directions. The ducks swim at 1.1 m/s and the goose swims with a speed of 1.3 m/s. Strategy: The total momentum of the three birds points to the right, in the direction the goose is swimming. That mea ...
... into a duck pond. Two 4.0-kg ducks and a 7.6-kg goose paddle rapidly toward the bread from opposite directions. The ducks swim at 1.1 m/s and the goose swims with a speed of 1.3 m/s. Strategy: The total momentum of the three birds points to the right, in the direction the goose is swimming. That mea ...
Chapter 19 - Aerostudents
... Problem 19.4 The space station is initially not rotating. Its reaction control system exerts a constant couple on it until it has rotated 90◦ , then exerts a constant couple of the same magnitude in the opposite direction so that its angular velocity has decreased to zero when it has undergone a to ...
... Problem 19.4 The space station is initially not rotating. Its reaction control system exerts a constant couple on it until it has rotated 90◦ , then exerts a constant couple of the same magnitude in the opposite direction so that its angular velocity has decreased to zero when it has undergone a to ...
Chapter 10 Elasticity & Oscillations
... drives the object to move further. If the energy during the period of aerodynamic excitation is larger than the natural damping of the system, the level of vibration will increase, resulting in self-exciting oscillation. The vibration levels can thus build up and are only limited when the aerodynami ...
... drives the object to move further. If the energy during the period of aerodynamic excitation is larger than the natural damping of the system, the level of vibration will increase, resulting in self-exciting oscillation. The vibration levels can thus build up and are only limited when the aerodynami ...
The Hopping Hoop
... Exercise 1 formally defines the center of mass. We show, in exercise 2, that the trajectory of the center of mass during the initial rolling-without-slipping phase must be a cycloid. After a brief review of the relevant physics, we proceed to write down, in exercises 3 and 4, the three differential ...
... Exercise 1 formally defines the center of mass. We show, in exercise 2, that the trajectory of the center of mass during the initial rolling-without-slipping phase must be a cycloid. After a brief review of the relevant physics, we proceed to write down, in exercises 3 and 4, the three differential ...
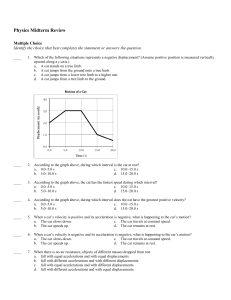
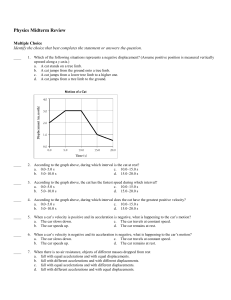
Physics Midterm Review Multiple Choice Identify the choice that best
... 38. Describe the graph of the vertical component of velocity versus time for the motion of the ball shown in the figure above. Identify any constants that would appear in the graph. 39. Why is force not a scalar quantity? 40. A block of wood supported by two concrete blocks is chopped in half by a k ...
... 38. Describe the graph of the vertical component of velocity versus time for the motion of the ball shown in the figure above. Identify any constants that would appear in the graph. 39. Why is force not a scalar quantity? 40. A block of wood supported by two concrete blocks is chopped in half by a k ...
Knowledge Check (Answer Key)
... fundamental or primary dimensions are mass, length, and time. It is necessary that you understand these three fundamental units, as they form the foundation for many concepts and principles presented later in this lesson. Fundamental Dimensions Mass: Mass is the amount of material present in an obje ...
... fundamental or primary dimensions are mass, length, and time. It is necessary that you understand these three fundamental units, as they form the foundation for many concepts and principles presented later in this lesson. Fundamental Dimensions Mass: Mass is the amount of material present in an obje ...
Persson2006-Contact_mechanics_for_randomly_rough_+
... the nominal contact area A0 , and made up from many small Hertzian-like asperity contact regions. This formulation has two drawbacks. First it neglects the interaction between the different contact regions. That is, if an asperity is squeezed against a flat hard surface it will deform not just local ...
... the nominal contact area A0 , and made up from many small Hertzian-like asperity contact regions. This formulation has two drawbacks. First it neglects the interaction between the different contact regions. That is, if an asperity is squeezed against a flat hard surface it will deform not just local ...
1st semester EXAM review and key
... 72. A rope attached to an engine pulls a 240 N crate up an 14.7° ramp at constant speed. The coefficient of kinetic friction for the surfaces of the crate and ramp is 0.32. What is the magnitude of the force that the rope exerts on the crate parallel to the ramp? 73. A roller coaster car goes over t ...
... 72. A rope attached to an engine pulls a 240 N crate up an 14.7° ramp at constant speed. The coefficient of kinetic friction for the surfaces of the crate and ramp is 0.32. What is the magnitude of the force that the rope exerts on the crate parallel to the ramp? 73. A roller coaster car goes over t ...
Mechanical System Elements
... • Power input to the device is positive since the force and velocity have the same sign. • It is impossible for the applied force and resulting velocity to have opposite signs. • Thus, a damper can never supply power to another device; Power is always positive. • A spring absorbs power and stores e ...
... • Power input to the device is positive since the force and velocity have the same sign. • It is impossible for the applied force and resulting velocity to have opposite signs. • Thus, a damper can never supply power to another device; Power is always positive. • A spring absorbs power and stores e ...
Lecture Notes on Classical Mechanics for Physics 106ab Sunil
... The reader will no doubt ask the question I asked myself many times while writing these notes: why bother? There are a large number of mechanics textbooks available all covering this very standard material, complete with worked examples and end-of-chapter problems. I can only defend myself by saying ...
... The reader will no doubt ask the question I asked myself many times while writing these notes: why bother? There are a large number of mechanics textbooks available all covering this very standard material, complete with worked examples and end-of-chapter problems. I can only defend myself by saying ...
PM6-93
... [As an aside, it should be noted that the transfer of metal which occurs when one metal is slid on another (which can occur in screwing or hammering) is of relevance in bone surgery. Since transfer can occur, it is very important to use tools of the same material as the metal plates etc. used to rep ...
... [As an aside, it should be noted that the transfer of metal which occurs when one metal is slid on another (which can occur in screwing or hammering) is of relevance in bone surgery. Since transfer can occur, it is very important to use tools of the same material as the metal plates etc. used to rep ...
Chapter 14
... In this equation, k is the spring constant, which depends on the stiffness and other properties of the spring, and x is the distance that the spring is stretched from its equilibrium position. Not all springs obey Hooke’s law, but many do. Those that do are called elastic. Potential energy When a fo ...
... In this equation, k is the spring constant, which depends on the stiffness and other properties of the spring, and x is the distance that the spring is stretched from its equilibrium position. Not all springs obey Hooke’s law, but many do. Those that do are called elastic. Potential energy When a fo ...
Hunting oscillation

Hunting oscillation is a self-oscillation, usually unwanted, about an equilibrium. The expression came into use in the 19th century and describes how a system ""hunts"" for equilibrium. The expression is used to describe phenomena in such diverse fields as electronics, aviation, biology, and railway engineering.