6 Newton`s Second Law of Motion–Force and Acceleration
... Both liquids and gases are called fluids because they flow. • Fluid friction occurs as an object pushes aside the fluid it is moving through. • The friction of liquids is appreciable, even at low speeds. • Air resistance is the friction acting on something moving through air. ...
... Both liquids and gases are called fluids because they flow. • Fluid friction occurs as an object pushes aside the fluid it is moving through. • The friction of liquids is appreciable, even at low speeds. • Air resistance is the friction acting on something moving through air. ...
Investigation 2: Genetic Traits
... intelligent guy. He worked on developing calculus and physics at the same time. During his work, he came up with the basic ideas that are applied to the physics of most motion. The ideas have been tested and verified so many times over the years, that scientists now call them Newton's 3 Laws of Moti ...
... intelligent guy. He worked on developing calculus and physics at the same time. During his work, he came up with the basic ideas that are applied to the physics of most motion. The ideas have been tested and verified so many times over the years, that scientists now call them Newton's 3 Laws of Moti ...
Force and Motion
... toys out and played with them to see how they would work in “microgravity.” Could you imagine trying to shoot a foam ball through a hoop while floating around in the space shuttle? How about running a toy car around a loop track – would that work? This chapter will help you use laws of motion to exp ...
... toys out and played with them to see how they would work in “microgravity.” Could you imagine trying to shoot a foam ball through a hoop while floating around in the space shuttle? How about running a toy car around a loop track – would that work? This chapter will help you use laws of motion to exp ...
pptx - Institute of Nuclear and Particle Physics
... Particle Detectors… Avalanche Multiplication When a particle passes through matter, it creates just a few electrons/ions or photons But the best we can do is to detect signals of the order of nV in a 100 Ohm resistor which correspond to I= U/R= 10-9 /100 = 10-11 A = 108 electrons. s-1 ...
... Particle Detectors… Avalanche Multiplication When a particle passes through matter, it creates just a few electrons/ions or photons But the best we can do is to detect signals of the order of nV in a 100 Ohm resistor which correspond to I= U/R= 10-9 /100 = 10-11 A = 108 electrons. s-1 ...
TWGHs. Kap Yan Directors` College
... 3. Answers to Section A should be written in the spaces provided in this Question-Answer Book. Answers to Section B should be marked on the Multiple-choice Answer Sheet. 4. The diagrams in this paper are NOT necessarily drawn to scale. 5. The following contains a list of data, formulae and relations ...
... 3. Answers to Section A should be written in the spaces provided in this Question-Answer Book. Answers to Section B should be marked on the Multiple-choice Answer Sheet. 4. The diagrams in this paper are NOT necessarily drawn to scale. 5. The following contains a list of data, formulae and relations ...
Hooke`s Law
... masses on springs is applicable to a variety of other situations. The criterion for simple harmonic motion is the presence of a restoring force that is proportional to the displacement. Oscillating systems provide a good example of the law of conservation of energy. Consider the oscillatingmass-on-a ...
... masses on springs is applicable to a variety of other situations. The criterion for simple harmonic motion is the presence of a restoring force that is proportional to the displacement. Oscillating systems provide a good example of the law of conservation of energy. Consider the oscillatingmass-on-a ...
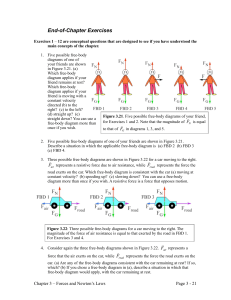
Chapter 3: Problems
... Figure 3.25: Two situations involving two boxes placed mass of the large box is five times side-by-side on a frictionless surface, for Exercises 18 – 20. larger than that of the small box. You then exert a horizontal force F directed right on the large box. Sketch a free-body diagram for (a) the two ...
... Figure 3.25: Two situations involving two boxes placed mass of the large box is five times side-by-side on a frictionless surface, for Exercises 18 – 20. larger than that of the small box. You then exert a horizontal force F directed right on the large box. Sketch a free-body diagram for (a) the two ...
Newton`s Laws Multiple Choice: 1. The resistance of an object to
... f. An object can experience two or more forces and not accelerate. g. A contact force results from the physical contact between two objects. h. A field force results from the action of two objects which are positioned some distance away. i. Spring and tension forces are examples of field forces. j. ...
... f. An object can experience two or more forces and not accelerate. g. A contact force results from the physical contact between two objects. h. A field force results from the action of two objects which are positioned some distance away. i. Spring and tension forces are examples of field forces. j. ...
t = 0
... •The acceleration is proportional to the position of the block, and its direction is opposite the direction of the displacement from the equilibrium position. •Systems that behave in this way is called Simple Harmonic Motion. •Object moves with Simple Harmonic Motion its acceleration is proportional ...
... •The acceleration is proportional to the position of the block, and its direction is opposite the direction of the displacement from the equilibrium position. •Systems that behave in this way is called Simple Harmonic Motion. •Object moves with Simple Harmonic Motion its acceleration is proportional ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.