Name
... 9. What is the difference between speed and velocity? Write an example of an object that has speed and one that has velocity. ...
... 9. What is the difference between speed and velocity? Write an example of an object that has speed and one that has velocity. ...
here - Physics at PMB
... In the previous section we studied kinematic which is the study of objects in motion disregarding the force that initiated the motion. However, in this section we pay our attention to the force that causes the motion. In particular, we will study the dynamics of an object, which is the study of moti ...
... In the previous section we studied kinematic which is the study of objects in motion disregarding the force that initiated the motion. However, in this section we pay our attention to the force that causes the motion. In particular, we will study the dynamics of an object, which is the study of moti ...
Chapter 7
... 1. In circular motion, the centripetal acceleration is directed 1. toward the center of the circle. 2. away from the center of the circle. 3. either of the above 4. neither of the above 2. Which is one of Kepler's laws? 1. The gravitational attraction of Earth and the Sun provides a centripetal acc ...
... 1. In circular motion, the centripetal acceleration is directed 1. toward the center of the circle. 2. away from the center of the circle. 3. either of the above 4. neither of the above 2. Which is one of Kepler's laws? 1. The gravitational attraction of Earth and the Sun provides a centripetal acc ...
Newton`s Second Law File
... License. This license gives you permission to copy, share and/or adapt these works, with appropriate attribution, under an identical, similar, or compatible license. See http://creativecommons.org/licenses/by-sa/3.0/ for more information. ...
... License. This license gives you permission to copy, share and/or adapt these works, with appropriate attribution, under an identical, similar, or compatible license. See http://creativecommons.org/licenses/by-sa/3.0/ for more information. ...
Langevin Equation
... dynamics of the particle, F is a series of randomly spaced spikes or delta functions—a very nasty looking function! However we are interested in the effect on the time scale M/γ during which many molecular collisions occur, and on this sort of time scale the noise force behaves as a Gaussian random ...
... dynamics of the particle, F is a series of randomly spaced spikes or delta functions—a very nasty looking function! However we are interested in the effect on the time scale M/γ during which many molecular collisions occur, and on this sort of time scale the noise force behaves as a Gaussian random ...
Balanced Forces
... Centripetal Force Centripetal Force: The ____________________exerted toward the center of a curved path. Earth’s gravity exerts a centripetal force on the Moon that keeps it in a nearly ___________________orbit. Falling Objects on Earth Near Earth’s surface acceleration due to gravity is 9 ...
... Centripetal Force Centripetal Force: The ____________________exerted toward the center of a curved path. Earth’s gravity exerts a centripetal force on the Moon that keeps it in a nearly ___________________orbit. Falling Objects on Earth Near Earth’s surface acceleration due to gravity is 9 ...
Physics 235 Chapter 8 Central-Force Motion
... In general, this equation has two solutions, and the orbit is confined between a minimum and maximum value of r. Under certain conditions, there is only a single solution, and in that case the orbit is circular. Using the orbital equation we can determine the change in the polar angle when the radiu ...
... In general, this equation has two solutions, and the orbit is confined between a minimum and maximum value of r. Under certain conditions, there is only a single solution, and in that case the orbit is circular. Using the orbital equation we can determine the change in the polar angle when the radiu ...
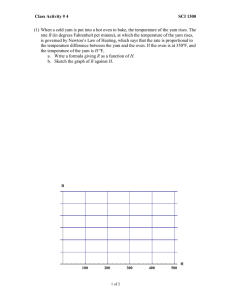
The following table converts degrees Fahrenheit to degrees
... Motion, F=m a, says that the net downward force, F, on the body is proportional to its downward acceleration, a. The net force, F, consists of the force due to gravity, Fg, which acts downward, minus the air resistance, Fr, which acts upward. The force due to gravity is m g, where g is a constant. A ...
... Motion, F=m a, says that the net downward force, F, on the body is proportional to its downward acceleration, a. The net force, F, consists of the force due to gravity, Fg, which acts downward, minus the air resistance, Fr, which acts upward. The force due to gravity is m g, where g is a constant. A ...
February 11 - Trimble County Schools
... Math RTI • Finish and go over Bananas WKT • Slope Intercept form ...
... Math RTI • Finish and go over Bananas WKT • Slope Intercept form ...
TAKS Obj 5
... Newton’s 2nd Law of Motion The greater the mass of an object, the greater the force required to change its motion. ...
... Newton’s 2nd Law of Motion The greater the mass of an object, the greater the force required to change its motion. ...
Physics Review
... Acceleration of an object depends on its mass and the size of the force acting on the object. F = m x a Ex. The dump truck takes longer to stop at a light than the little sports car. 11. What is Newton’s Third Law of Motion? Give a real world example For every action, there is an equal and opposite ...
... Acceleration of an object depends on its mass and the size of the force acting on the object. F = m x a Ex. The dump truck takes longer to stop at a light than the little sports car. 11. What is Newton’s Third Law of Motion? Give a real world example For every action, there is an equal and opposite ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.