Vectors - Light and Matter
... is good for handwritten equations, but is unattractive in a printed book, so books use boldface, F, to represent vectors. After this point, I’ll use boldface for vectors throughout this book. Quantities can be classified as vectors or scalars. In a phrase like “a to the northeast,” it makes sense to ...
... is good for handwritten equations, but is unattractive in a printed book, so books use boldface, F, to represent vectors. After this point, I’ll use boldface for vectors throughout this book. Quantities can be classified as vectors or scalars. In a phrase like “a to the northeast,” it makes sense to ...
Final Exam Review
... A baseball after it is hit with a bat A small pebble at rest A car traveling on a highway ...
... A baseball after it is hit with a bat A small pebble at rest A car traveling on a highway ...
Chapter M1
... unbalanced force on the apple made the apple fall. • He also reasoned that an unbalanced force on the moon kept the moon moving around the Earth. • He proposed that these two forces are actually the same force––gravity. ...
... unbalanced force on the apple made the apple fall. • He also reasoned that an unbalanced force on the moon kept the moon moving around the Earth. • He proposed that these two forces are actually the same force––gravity. ...
03BC VA-Kinem-Fall-Newt WS08
... 32. State which of Newton’s Laws of Motion is most closely associated with each of the following. (a) action-reaction (Answer: Third Law) (b) When a car makes a sudden stop, seatbelts are needed to protect passengers. (Answer: First Law) (c) When you step off a boat and onto a dock, the boat tends ...
... 32. State which of Newton’s Laws of Motion is most closely associated with each of the following. (a) action-reaction (Answer: Third Law) (b) When a car makes a sudden stop, seatbelts are needed to protect passengers. (Answer: First Law) (c) When you step off a boat and onto a dock, the boat tends ...
Version 055 – Midterm 1
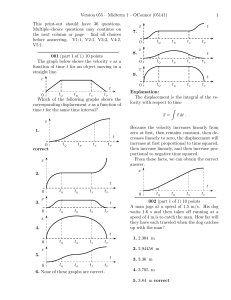
... Find Sdown , the scale reading when the elevator is moving downward with constant velocity, in terms of Ss . 1. Sdown = 2. Sdown = 3. Sdown = 4. Sdown = 5. Sdown = ...
... Find Sdown , the scale reading when the elevator is moving downward with constant velocity, in terms of Ss . 1. Sdown = 2. Sdown = 3. Sdown = 4. Sdown = 5. Sdown = ...
0175 Lecture Notes - Force of Impact Equation Derivation
... In order to say the force of impact during the collision was equal to the net force during the collision, we needed to use the Impulse Approximation. Impulse Approximation: During the short time interval of a collision, the force of impact is much larger than all the other forces, therefore we can c ...
... In order to say the force of impact during the collision was equal to the net force during the collision, we needed to use the Impulse Approximation. Impulse Approximation: During the short time interval of a collision, the force of impact is much larger than all the other forces, therefore we can c ...
The Classical Electromagnetism of Particle Detection
... The three components of A each have similar solutions. The first term describes outgoing waves emitted by the charges near the origin and is called the Retarded Potential. The second term describes incoming waves absorbed by the charges near the originand is called the Advanced Potential.. ...
... The three components of A each have similar solutions. The first term describes outgoing waves emitted by the charges near the origin and is called the Retarded Potential. The second term describes incoming waves absorbed by the charges near the originand is called the Advanced Potential.. ...
Unit 4 Packet (Labs)
... independent of the path between the object’s initial and final positions. (Gravitational force is a conservative force) A force is conservative when it does no net work on an object moving around a closed path, starting and ending at the same point… (ex: riding a roller coaster in a complete loop) A ...
... independent of the path between the object’s initial and final positions. (Gravitational force is a conservative force) A force is conservative when it does no net work on an object moving around a closed path, starting and ending at the same point… (ex: riding a roller coaster in a complete loop) A ...
CHAPTER 4
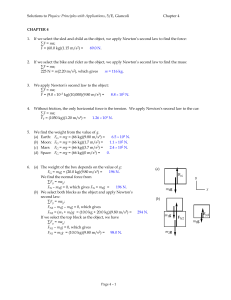
... FTmax = m(a + g) = (1200 kg)(0.0600 + 1)(9.80 m/s2) = 5.04104 N. The minimum tension will be exerted by the motor when the elevator is accelerating downward. We write ∑F = ma from the force diagram for the car: y-component: FTmin – mg = ma, or FTmin = m(a + g) = (1200 kg)(– 0.0600 + 1)(9.80 m/s2 ...
... FTmax = m(a + g) = (1200 kg)(0.0600 + 1)(9.80 m/s2) = 5.04104 N. The minimum tension will be exerted by the motor when the elevator is accelerating downward. We write ∑F = ma from the force diagram for the car: y-component: FTmin – mg = ma, or FTmin = m(a + g) = (1200 kg)(– 0.0600 + 1)(9.80 m/s2 ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.