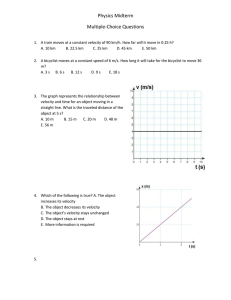
Unit 2 AP Forces Practice Problems
... 26. *A 2 Kg mass and a 3 Kg mass are attached to a massless cord that passes over a frictionless pulley. The masses are free to move. a. Draw the scenario, showing all forces acting on both masses. (in class) b. What direction does the smaller mass move? (up) c. What is the acceleration of the syste ...
... 26. *A 2 Kg mass and a 3 Kg mass are attached to a massless cord that passes over a frictionless pulley. The masses are free to move. a. Draw the scenario, showing all forces acting on both masses. (in class) b. What direction does the smaller mass move? (up) c. What is the acceleration of the syste ...
Unit 2 AP Forces Practice Problems
... 26. *A 2 Kg mass and a 3 Kg mass are attached to a massless cord that passes over a frictionless pulley. The masses are free to move. a. Draw the scenario, showing all forces acting on both masses. (in class) b. What direction does the smaller mass move? (up) c. What is the acceleration of the syste ...
... 26. *A 2 Kg mass and a 3 Kg mass are attached to a massless cord that passes over a frictionless pulley. The masses are free to move. a. Draw the scenario, showing all forces acting on both masses. (in class) b. What direction does the smaller mass move? (up) c. What is the acceleration of the syste ...
PS02H - willisworldbio
... • ________ is the rate of change of velocity. When the _______ of an object changes, the object is accelerating. • A change in velocity can be either a change in how _____ something is moving, or a change in the ______ it is moving. • Acceleration occurs when an object changes its _____, it's _____ ...
... • ________ is the rate of change of velocity. When the _______ of an object changes, the object is accelerating. • A change in velocity can be either a change in how _____ something is moving, or a change in the ______ it is moving. • Acceleration occurs when an object changes its _____, it's _____ ...
Chapter 7: Kinetic Energy and Work
... (a) We know that the total work done on a body equals the change in its kinetic energy. Since we have only a friction force, then the total work is due to it. Hence, we have Wf =ΔK =K2 – K1= ½ m (v22 – v12) = ½ × 1 × (22 – 42) = -6 J (b) It is well known that the work done by the friction force is g ...
... (a) We know that the total work done on a body equals the change in its kinetic energy. Since we have only a friction force, then the total work is due to it. Hence, we have Wf =ΔK =K2 – K1= ½ m (v22 – v12) = ½ × 1 × (22 – 42) = -6 J (b) It is well known that the work done by the friction force is g ...
356 Linear Kinetics
... • As the block moves along the table, there still is a frictional force that resists motion. • Sliding and rolling friction are types of ...
... • As the block moves along the table, there still is a frictional force that resists motion. • Sliding and rolling friction are types of ...
Force and Motion
... with the most mass will have the smallest acceleration and the one with the least mass will have the greatest acceleration. If you apply the same force to several different objects, the one with the most mass will have the smallest acceleration and the one with the least mass will have the greatest ...
... with the most mass will have the smallest acceleration and the one with the least mass will have the greatest acceleration. If you apply the same force to several different objects, the one with the most mass will have the smallest acceleration and the one with the least mass will have the greatest ...
The Physics of the Mobile
... Note that one torque will provide a rotational force in the counterclockwise direction (F1) while the other force will provide a rotational force in the clockwise direction (F2) d1 ...
... Note that one torque will provide a rotational force in the counterclockwise direction (F1) while the other force will provide a rotational force in the clockwise direction (F2) d1 ...
PPT
... magnetic field such that a positively charged particle with initial velocity v travels straight through and exits the other side. ...
... magnetic field such that a positively charged particle with initial velocity v travels straight through and exits the other side. ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.