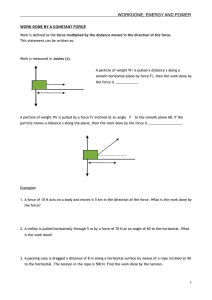
VU2 Movement 2008
... It is that current which produces travels, in a vacuum, a force of 2 x 10-7 N between two in 1/299,792,458th of parallel wires which are 1 metre a second. apart in a vacuum. ...
... It is that current which produces travels, in a vacuum, a force of 2 x 10-7 N between two in 1/299,792,458th of parallel wires which are 1 metre a second. apart in a vacuum. ...
9 - tucek
... -the equality of the momenta before and after the collision also means that the sum of the components of the vectors before and after the collision must be equal -if the x-axis in the direction of the initial momentum then the ycomponent of the initial momentum is equal to zero -the sum of the fina ...
... -the equality of the momenta before and after the collision also means that the sum of the components of the vectors before and after the collision must be equal -if the x-axis in the direction of the initial momentum then the ycomponent of the initial momentum is equal to zero -the sum of the fina ...
Magnetism and Electromagnetic Forces
... In each case, the shaded region contains a uniform magnetic field that may point either into the page or out of the page. A charged particle moves through .the region along the path indicated. A l l of the charged particles have the same mass and enter the region with the same initial speed. ...
... In each case, the shaded region contains a uniform magnetic field that may point either into the page or out of the page. A charged particle moves through .the region along the path indicated. A l l of the charged particles have the same mass and enter the region with the same initial speed. ...
Unit 2 Review Session Part 1
... use for work or energy? • Work and energy are both measured using the unit Joule. • 1 Joule = 1 Newton of force applied over a distance of 1 meter. ...
... use for work or energy? • Work and energy are both measured using the unit Joule. • 1 Joule = 1 Newton of force applied over a distance of 1 meter. ...
Lab 4: Friction
... 2. Use a triple beam balance to find the mass of the wood block, and record it in your data table. Calculate the weight of the block and record it in your data table. 3. Keeping the board horizontal, place the block on top of the board, connect the string to it, and run the string over the pulley. ...
... 2. Use a triple beam balance to find the mass of the wood block, and record it in your data table. Calculate the weight of the block and record it in your data table. 3. Keeping the board horizontal, place the block on top of the board, connect the string to it, and run the string over the pulley. ...
CHAPTER 4
... 16. (II) A person pushes a 14.5-kg lawn mower at constant speed with a force of 88.0 N directed along the handle, which is at an angle of 45.0o to the horizontal (Fig. 4-40). (a) Draw the free-body diagram showing all forces acting on the mower. Calculate (b) the horizontal retarding force on the mo ...
... 16. (II) A person pushes a 14.5-kg lawn mower at constant speed with a force of 88.0 N directed along the handle, which is at an angle of 45.0o to the horizontal (Fig. 4-40). (a) Draw the free-body diagram showing all forces acting on the mower. Calculate (b) the horizontal retarding force on the mo ...
Chapter 5 Examples
... Example 12: final. Equating: (3) = (4) and Solving for a m1 g + m1 a = m 2 g – m 2 a m1 a + m 2 a = m 2 g – m1 g a (m1 + m2) = (m2 – m1)g ...
... Example 12: final. Equating: (3) = (4) and Solving for a m1 g + m1 a = m 2 g – m 2 a m1 a + m 2 a = m 2 g – m1 g a (m1 + m2) = (m2 – m1)g ...
Work and Energy
... W Fx mgy This energy can be converted to kinetic energy if the object is then allowed to fall back to its ...
... W Fx mgy This energy can be converted to kinetic energy if the object is then allowed to fall back to its ...
Chapter 5 Work and Energy
... and over the displacement s, the speed of the car will increase. Newton's 2nd law: acceleration of the car, a = F mCar Starting with velocity v0 , find the final speed. ...
... and over the displacement s, the speed of the car will increase. Newton's 2nd law: acceleration of the car, a = F mCar Starting with velocity v0 , find the final speed. ...
Rigid Body Simulation (1)
... • Because a rigid body can undergo only rotation and translation, we define the shape of a rigid body in terms of a fixed and unchanging space called body space. • Given a geometric description of the body in body space, we use x(t) and R(t) to transform the body-space description into world space ...
... • Because a rigid body can undergo only rotation and translation, we define the shape of a rigid body in terms of a fixed and unchanging space called body space. • Given a geometric description of the body in body space, we use x(t) and R(t) to transform the body-space description into world space ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.