Introduction to Lattice Field Theory
... For a new formulation of quantum mechanics we have a trivial algorithm for computing the energy. It exploits the simple fact that given a randomly chosen unit vector |φi, the matrix element hφ| T n |φi tends to λn0 as n → ∞. 1. Choose a source. At one time slice construct a random linear combination ...
... For a new formulation of quantum mechanics we have a trivial algorithm for computing the energy. It exploits the simple fact that given a randomly chosen unit vector |φi, the matrix element hφ| T n |φi tends to λn0 as n → ∞. 1. Choose a source. At one time slice construct a random linear combination ...
Path integral for the quantum harmonic oscillator using elementary
... oscillator using Feynman’s path integral. Though the details of the calculation are involved, the general approach uses only matrix diagonalization and well-known integrals, techniques which an advanced undergraduate should understand. The full propagator, including both the prefactor and the classi ...
... oscillator using Feynman’s path integral. Though the details of the calculation are involved, the general approach uses only matrix diagonalization and well-known integrals, techniques which an advanced undergraduate should understand. The full propagator, including both the prefactor and the classi ...
Renormalization and quantum field theory
... Feynman propagators or advanced and retarded propagators that can have more complicated wave front sets. For most common cut propagators in Minkowski space, this follows from the fact that their Fourier transforms have support in the positive cone. The condition about being expressible in terms of s ...
... Feynman propagators or advanced and retarded propagators that can have more complicated wave front sets. For most common cut propagators in Minkowski space, this follows from the fact that their Fourier transforms have support in the positive cone. The condition about being expressible in terms of s ...
Calculating gg → tt + jets at Tree Level
... predictions are required. We are interested in Feynman diagrammatic approach of gg −→ tt + n gluons which is a partonic component of pp −→ tt + jets. The results will provide background for future discoveries in LHC. The aim of this project is to provide a complete calculation at tree-level for gg − ...
... predictions are required. We are interested in Feynman diagrammatic approach of gg −→ tt + n gluons which is a partonic component of pp −→ tt + jets. The results will provide background for future discoveries in LHC. The aim of this project is to provide a complete calculation at tree-level for gg − ...
PPT - Physics
... interaction can be varied but adjusting the cut-off for the MPI. One can also adjust whether the probability of a MPI depends on the PT of the hard scattering, PT(hard) (constant cross section or varying with impact parameter). One can adjust the color connections and flavor of the MPI (singlet ...
... interaction can be varied but adjusting the cut-off for the MPI. One can also adjust whether the probability of a MPI depends on the PT of the hard scattering, PT(hard) (constant cross section or varying with impact parameter). One can adjust the color connections and flavor of the MPI (singlet ...
In the early 1930s, the relativistic electron
... usual interpretation of quantum theories, a submicroscopic observer – say Alice –, then the cat – our propagator – will reveal peculiar behaviours. The case is that the propagator does not vanish for a space-like separation. This means we would have an interaction between space-time points not conne ...
... usual interpretation of quantum theories, a submicroscopic observer – say Alice –, then the cat – our propagator – will reveal peculiar behaviours. The case is that the propagator does not vanish for a space-like separation. This means we would have an interaction between space-time points not conne ...
Feynman Diagrams in Quantum Mechanics
... of a graph, with no stray lines leaving. The general procedure is to first figure out which diagrams are relevant to the problem being solved, and then use some Feynman rules to calculate a value for each diagram. The values are then added together, with certain weights, to evaluate the desired expe ...
... of a graph, with no stray lines leaving. The general procedure is to first figure out which diagrams are relevant to the problem being solved, and then use some Feynman rules to calculate a value for each diagram. The values are then added together, with certain weights, to evaluate the desired expe ...
Feynman Diagrams for Beginners
... and |M|2 is the Feynman invariant amplitude averaged over unmeasured particle spins (see Section 6.1). The dimension of M, in units of energy, is • for decays [M] = 3 − n • for scattering of two particles [M] = 2 − n where n is the number of produced particles. So calculation of some observable quan ...
... and |M|2 is the Feynman invariant amplitude averaged over unmeasured particle spins (see Section 6.1). The dimension of M, in units of energy, is • for decays [M] = 3 − n • for scattering of two particles [M] = 2 − n where n is the number of produced particles. So calculation of some observable quan ...
Lagrangian, functional integrals, effective action
... the condition of being k-vertex-connected is stronger than that of being k-edge-connected. The terminology more commonly in use in the physics literature is the following. Definition 1.5.2. For k ≥ 2 a (k + 1)-edge-connected graph is also called k-particle-irreducible (kPI). For k = 1, a 2-edge-conn ...
... the condition of being k-vertex-connected is stronger than that of being k-edge-connected. The terminology more commonly in use in the physics literature is the following. Definition 1.5.2. For k ≥ 2 a (k + 1)-edge-connected graph is also called k-particle-irreducible (kPI). For k = 1, a 2-edge-conn ...
Numerical Methods Project: Feynman path integrals in quantum
... where |ai are the eigenkets. From this expression it is readily seen that a fourie transform of this time series’s trace would yield peaks at the energilevels divided by 2π. Since the trace is independent of basis we use this observation to find the energies from the Feynman propagator. To construct ...
... where |ai are the eigenkets. From this expression it is readily seen that a fourie transform of this time series’s trace would yield peaks at the energilevels divided by 2π. Since the trace is independent of basis we use this observation to find the energies from the Feynman propagator. To construct ...
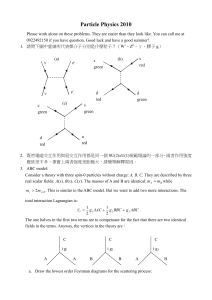
Particle Physics
... θ and initial momentum magnitude p p1 p2 . Only its relations with θ and p are needed. You can drop all the multiplicative constants. Comment: This is the result for a structure-less scattering. Compare it to the answers in 3c, 3d where there is a propagating mediating particle. From the experim ...
... θ and initial momentum magnitude p p1 p2 . Only its relations with θ and p are needed. You can drop all the multiplicative constants. Comment: This is the result for a structure-less scattering. Compare it to the answers in 3c, 3d where there is a propagating mediating particle. From the experim ...
The structure of perturbative quantum gauge theories
... Renormalization as a decomposition in G The above Hopf algebra H is the algebraic structure underlying the recursive procedure of renormalization. In fact, for a character Uz : H → C, there exists a character Cz : H → C (‘counterterm’) defined for z 6= 0, such that Rz = Cz ∗ Uz is finite at z = 0 [ ...
... Renormalization as a decomposition in G The above Hopf algebra H is the algebraic structure underlying the recursive procedure of renormalization. In fact, for a character Uz : H → C, there exists a character Cz : H → C (‘counterterm’) defined for z 6= 0, such that Rz = Cz ∗ Uz is finite at z = 0 [ ...
physics 151h: honors mechanics
... Last week, we began a discussion the theoretical basis for some of our understanding of the interactions among elementary particles. We began with an introduction to Lagrangian field theory, which helps introduce the notation. We then discussed the Dirac equation and the notion of local gauge invari ...
... Last week, we began a discussion the theoretical basis for some of our understanding of the interactions among elementary particles. We began with an introduction to Lagrangian field theory, which helps introduce the notation. We then discussed the Dirac equation and the notion of local gauge invari ...
physics 151h: honors mechanics
... Last week, we began a discussion the theoretical basis for some of our understanding of the interactions among elementary particles. We began with an introduction to Lagrangian field theory, which helps introduce the notation. We now discuss the Dirac equation and the notion of local gauge invarianc ...
... Last week, we began a discussion the theoretical basis for some of our understanding of the interactions among elementary particles. We began with an introduction to Lagrangian field theory, which helps introduce the notation. We now discuss the Dirac equation and the notion of local gauge invarianc ...
How Feynman Diagrams Almost Saved Space
... which also have several other attractive features, achieve that cancellation. Another thing we’ve learned is that in addition to fluctuating fields, the vacuum contains nonfluctuating fields, often called “condensates.” One such condensate is the so-called sigma condensate; another is the Higgs cond ...
... which also have several other attractive features, achieve that cancellation. Another thing we’ve learned is that in addition to fluctuating fields, the vacuum contains nonfluctuating fields, often called “condensates.” One such condensate is the so-called sigma condensate; another is the Higgs cond ...
Dia 1
... harmless ? Should the small-distance behavior provide answers? This was an important reason for studying the scaling behavior of gauge theories. What is their small-distance structure? If they stay regular, should the absence of 1-loop anomalies then not be sufficient to guarantee their absence at h ...
... harmless ? Should the small-distance behavior provide answers? This was an important reason for studying the scaling behavior of gauge theories. What is their small-distance structure? If they stay regular, should the absence of 1-loop anomalies then not be sufficient to guarantee their absence at h ...
Khatua, Bansal, and Shahar Reply: The preceding
... same, is thus neither “fortuitous” nor “puzzling.” Figure 15–7 of Ref. [3] describes the Aharonov-Bohm effect that further reveals the nontrivial topological nature of the vector potential, but the electron acquires an Aharonov-Bohm phase for both Figs. 15–7 and 15–8 of Ref. [3]. The preceding Comme ...
... same, is thus neither “fortuitous” nor “puzzling.” Figure 15–7 of Ref. [3] describes the Aharonov-Bohm effect that further reveals the nontrivial topological nature of the vector potential, but the electron acquires an Aharonov-Bohm phase for both Figs. 15–7 and 15–8 of Ref. [3]. The preceding Comme ...
Feynman Diagrams
... Solid lines are charged fermions: ■ particle: arrow in same direction as time ■ antiparticle: arrow opposite direction as time Wavy (or dashed) lines are photons. At each vertex there is a coupling constant. Quantum numbers are conserved at a vertex: ■ electric charge, lepton number… “Virtua ...
... Solid lines are charged fermions: ■ particle: arrow in same direction as time ■ antiparticle: arrow opposite direction as time Wavy (or dashed) lines are photons. At each vertex there is a coupling constant. Quantum numbers are conserved at a vertex: ■ electric charge, lepton number… “Virtua ...
Richard Feynman

Richard Phillips Feynman, (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman, jointly with Julian Schwinger and Sin-Itiro Tomonaga, received the Nobel Prize in Physics in 1965. He developed a widely used pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World he was ranked as one of the ten greatest physicists of all time.He assisted in the development of the atomic bomb during World War II and became known to a wide public in the 1980s as a member of the Rogers Commission, the panel that investigated the Space Shuttle Challenger disaster. In addition to his work in theoretical physics, Feynman has been credited with pioneering the field of quantum computing, and introducing the concept of nanotechnology. He held the Richard Chace Tolman professorship in theoretical physics at the California Institute of Technology.Feynman was a keen popularizer of physics through both books and lectures, including a 1959 talk on top-down nanotechnology called There's Plenty of Room at the Bottom, and the three-volume publication of his undergraduate lectures, The Feynman Lectures on Physics. Feynman also became known through his semi-autobiographical books Surely You're Joking, Mr. Feynman! and What Do You Care What Other People Think? and books written about him, such as Tuva or Bust! and Genius: The Life and Science of Richard Feynman by James Gleick.