Math for Game Programmers: Dual Numbers
... Operations are similar to complex numbers, however since ε2 = 0, we have: ...
... Operations are similar to complex numbers, however since ε2 = 0, we have: ...
(2) The student erred because the included the measures of angles
... (2) (2) The student erred because the included the measures of angles F, G, K, and N which are not angles of the polygon. Since these angles form a circle, the student can get the correct answer of 540 by subtracting 360 from the answer that they got. Another approach would be to divide the pentagon ...
... (2) (2) The student erred because the included the measures of angles F, G, K, and N which are not angles of the polygon. Since these angles form a circle, the student can get the correct answer of 540 by subtracting 360 from the answer that they got. Another approach would be to divide the pentagon ...
FINITENESS OF RANK INVARIANTS OF MULTIDIMENSIONAL
... this functional setting is not large enough to address the problems encountered in practical applications, and stability of persistence diagrams is revisited. The basic assumption to prove stability in [5] is the finiteness of persistent homology ranks, but the question of how achieving this is left ...
... this functional setting is not large enough to address the problems encountered in practical applications, and stability of persistence diagrams is revisited. The basic assumption to prove stability in [5] is the finiteness of persistent homology ranks, but the question of how achieving this is left ...
Lesson 14
... • The sum of the measure of interior angles of any triangle is 180°. • We can use this fact to help us figure out how many degrees are inside polygons. ...
... • The sum of the measure of interior angles of any triangle is 180°. • We can use this fact to help us figure out how many degrees are inside polygons. ...
Tyaglov_Fourier_and_Real_Analysis_Syllabus_Form
... The course is introduction to the theory of Fourier series and transform as well as to the theory of Lebesque integration. Fundamental ideas and rigorous proof will be presented. Topics of the course to be covered include Fourier series, their convergence and applications, Poisson kernel, Cesaro and ...
... The course is introduction to the theory of Fourier series and transform as well as to the theory of Lebesque integration. Fundamental ideas and rigorous proof will be presented. Topics of the course to be covered include Fourier series, their convergence and applications, Poisson kernel, Cesaro and ...
Finding the area of a Trapezoid
... Marianna makes a 5% commission on the appliances she sells. If she earns $600 in salary but needs to earn a total of $975 for her paycheck, how much merchandise will she have to sell? ...
... Marianna makes a 5% commission on the appliances she sells. If she earns $600 in salary but needs to earn a total of $975 for her paycheck, how much merchandise will she have to sell? ...
Circle and Shape Properties to know
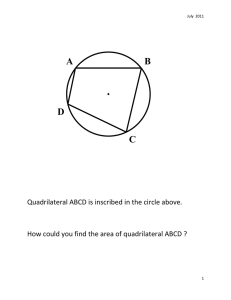
... The measure of the minor arc is equal to the measure of the central angle subtended by the arc. A central angle is the angle with endpoints on the arc of a circle and vertex at the centre. The measure of the inscribed angle subtended by an arc is equal to one-half the size of the arc. An inscribed a ...
... The measure of the minor arc is equal to the measure of the central angle subtended by the arc. A central angle is the angle with endpoints on the arc of a circle and vertex at the centre. The measure of the inscribed angle subtended by an arc is equal to one-half the size of the arc. An inscribed a ...
Exercise Sheet 4 - D-MATH
... c)* The sheaf of germs of holomorphic functions over C is Hausdorff and is a smooth manifold. The sheaf of germs of smooth real-valued functions over R is an extreme example of “non-Hausdorff manifold”. 3. Consider R with its usual differentiable structure, induced by the chart ϕ : R Ñ R, ϕpxq “ x, ...
... c)* The sheaf of germs of holomorphic functions over C is Hausdorff and is a smooth manifold. The sheaf of germs of smooth real-valued functions over R is an extreme example of “non-Hausdorff manifold”. 3. Consider R with its usual differentiable structure, induced by the chart ϕ : R Ñ R, ϕpxq “ x, ...
ON TAMAGAWA NUMBERS 1. Adele geometry Let X be an
... all p, i. e. for all but a finite number of p. The set XA of all adeles becomes a locally compact space and is called the adele space of X. We identify XQ as a subset of XA by the diagonal imbedding. If X is quasi-affine, XQ is discrete in XA. The adele geometry is the study of the pair (XA, XQ), to ...
... all p, i. e. for all but a finite number of p. The set XA of all adeles becomes a locally compact space and is called the adele space of X. We identify XQ as a subset of XA by the diagonal imbedding. If X is quasi-affine, XQ is discrete in XA. The adele geometry is the study of the pair (XA, XQ), to ...
PDF
... Theorem 1. Suppose X is a topological space. If K is a compact subset of X, C is a closed set in X, and C ⊆ K, then C is a compact set in X. The below proof follows e.g. [?]. A proof based on the finite intersection property is given in [?]. Proof. Let I be an indexing set and F = {Vα | α ∈ I} be an ...
... Theorem 1. Suppose X is a topological space. If K is a compact subset of X, C is a closed set in X, and C ⊆ K, then C is a compact set in X. The below proof follows e.g. [?]. A proof based on the finite intersection property is given in [?]. Proof. Let I be an indexing set and F = {Vα | α ∈ I} be an ...
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle, or finite cyclic groups. The Pontryagin duality theorem itself states that locally compact groups identify naturally with their bidual.The subject is named after Lev Semenovich Pontryagin who laid down the foundations for the theory of locally compact abelian groups and their duality during his early mathematical works in 1934. Pontryagin's treatment relied on the group being second-countable and either compact or discrete. This was improved to cover the general locally compact abelian groups by Egbert van Kampen in 1935 and André Weil in 1940.