Full Groups and Orbit Equivalence in Cantor Dynamics
... for example, [E1], [KT], and [Me]. We should point out that Dye’s theorem is a universal result as it holds in completely different dynamical setups. For example, there is a Borel version of Dye’s theorem [MilRos] established for full groups of Borel equivalence relations. The thesis of Miller [Mil] ...
... for example, [E1], [KT], and [Me]. We should point out that Dye’s theorem is a universal result as it holds in completely different dynamical setups. For example, there is a Borel version of Dye’s theorem [MilRos] established for full groups of Borel equivalence relations. The thesis of Miller [Mil] ...
complete lecture notes in a pdf file - Mathematics
... The aim of Book III is to introduce an axiomatic approach to set theory. Notice however that we do not include all axioms of set theory: instead, we only discuss several of the most basic axioms and focus on practicing how to form and prove simple formulas in “the language of set theory”. We also di ...
... The aim of Book III is to introduce an axiomatic approach to set theory. Notice however that we do not include all axioms of set theory: instead, we only discuss several of the most basic axioms and focus on practicing how to form and prove simple formulas in “the language of set theory”. We also di ...
duality of quantifiers ¬8xA(x) 9x¬A(x) ¬9xA(x) 8x¬A(x)
... There are problems that cannot be solved by computer programs (i.e. algorithms) even assuming unlimited time and space. What is an “algorithm”? The following are all equivalent: - C programs, scheme programs, Java programs . . . - Turing machines (Turing’s idea of an “algorithm”) ...
... There are problems that cannot be solved by computer programs (i.e. algorithms) even assuming unlimited time and space. What is an “algorithm”? The following are all equivalent: - C programs, scheme programs, Java programs . . . - Turing machines (Turing’s idea of an “algorithm”) ...
Programming with Classical Proofs
... if we are working in Church-style. This saves space, and the types can be deduced from the context. For formulas ', we will often write '(↵), which means that we can substitute ↵ with n simply by writing '(n). It does not necessarily imply that ↵ is the only free variable in '. Natural deduction pro ...
... if we are working in Church-style. This saves space, and the types can be deduced from the context. For formulas ', we will often write '(↵), which means that we can substitute ↵ with n simply by writing '(n). It does not necessarily imply that ↵ is the only free variable in '. Natural deduction pro ...
File
... straight line. If the distance between the first pole and the last pole is d metres find the distance between each pole. ...
... straight line. If the distance between the first pole and the last pole is d metres find the distance between each pole. ...
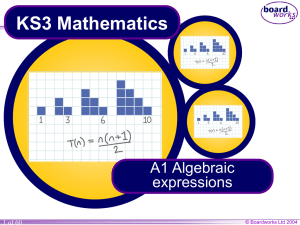
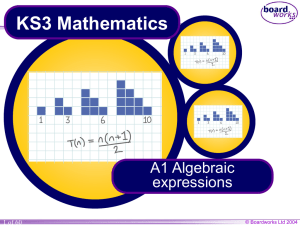
Simplifying algebra(7-9)
... but it doesnt. The terms 3x and 9x2 are similar in appearance but not like terms since the algebra is not identical. Some terms don’t look alike but they are. Consider 8ab + 9ba. Since ab means a × b and ba means b × a, if a = 3 and b = 5 we know that 3 × 5 is the same as 5 × 3. Hence, ab and ba are ...
... but it doesnt. The terms 3x and 9x2 are similar in appearance but not like terms since the algebra is not identical. Some terms don’t look alike but they are. Consider 8ab + 9ba. Since ab means a × b and ba means b × a, if a = 3 and b = 5 we know that 3 × 5 is the same as 5 × 3. Hence, ab and ba are ...
FACTORIZATION OF POLYNOMIALS 1. Polynomials in One
... √ ring Z is a finite process. The most naive method, trial division, requires n steps to find a factor of n. The next proposition and its corollary show, for example, that factorization in Z[X1 , · · · , Xn ] is also a finite process. Proposition 5.1. Let A be a UFD with a factoring algorithm. Then ...
... √ ring Z is a finite process. The most naive method, trial division, requires n steps to find a factor of n. The next proposition and its corollary show, for example, that factorization in Z[X1 , · · · , Xn ] is also a finite process. Proposition 5.1. Let A be a UFD with a factoring algorithm. Then ...
Formal Theories of Truth INTRODUCTION
... and the above equation is then an additional axiom of A. Alternatively, one can conceive dia as a metalinguistic abbreviation, which does not form part of the language L, but which is just short notation for a more complex expression. This situation will encountered in the following frequently. ...
... and the above equation is then an additional axiom of A. Alternatively, one can conceive dia as a metalinguistic abbreviation, which does not form part of the language L, but which is just short notation for a more complex expression. This situation will encountered in the following frequently. ...