A Mathematical Framework for Parallel Computing of Discrete
... Abstract: This paper presents a mathematical framework for a family of discrete-time discrete-frequency transforms in terms of matrix signal algebra. The matrix signal algebra is a mathematics environment composed of a signal space, a finite dimensional linear operators and special matrices where al ...
... Abstract: This paper presents a mathematical framework for a family of discrete-time discrete-frequency transforms in terms of matrix signal algebra. The matrix signal algebra is a mathematics environment composed of a signal space, a finite dimensional linear operators and special matrices where al ...
Lecture 6: Arithmetic COS / ELE 375
... implemented in naïve ways à Add at each step • Observe and optimize adding of zeros, use of space • Booth’s algorithm deals with signed and may be faster • Lots of other efforts made in speeding multiplication up • Consider multiplication by powers of 2 • Special case small integers ...
... implemented in naïve ways à Add at each step • Observe and optimize adding of zeros, use of space • Booth’s algorithm deals with signed and may be faster • Lots of other efforts made in speeding multiplication up • Consider multiplication by powers of 2 • Special case small integers ...
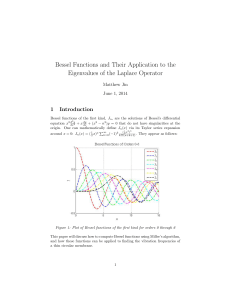
Bessel Functions and Their Application to the Eigenvalues of the
... Figure 5: This table compares the size of n and x against the amount of time it takes the downwards recurrence algorithm written for this project to compute Jn (x). Note that order of n and x is given in number of digits, so order 1 and 2 in this case refers to numbers ranging from 1 to 99, and 5 re ...
... Figure 5: This table compares the size of n and x against the amount of time it takes the downwards recurrence algorithm written for this project to compute Jn (x). Note that order of n and x is given in number of digits, so order 1 and 2 in this case refers to numbers ranging from 1 to 99, and 5 re ...
Robust Ray Intersection with Interval Arithmetic
... root-isolation algorithms conform to this paradigm, whether they use Descarte’s Rule, Lipschitz conditions, or interval arithmetic to test for root inclusion. The algorithm above is slightly different than the one described by Moore which assumes that root refinement will also be performed by an int ...
... root-isolation algorithms conform to this paradigm, whether they use Descarte’s Rule, Lipschitz conditions, or interval arithmetic to test for root inclusion. The algorithm above is slightly different than the one described by Moore which assumes that root refinement will also be performed by an int ...
SAXS Software
... Per step, 103 atoms means ~106 terms, which could result in an error term of up to 105. ...
... Per step, 103 atoms means ~106 terms, which could result in an error term of up to 105. ...
linear-system
... While conditions for convergence of this method are readily established, useful theoretical estimates of the rate of convergence of the Kaczmarz method (or more generally of the alternating projection method for linear subspaces) are difficult to obtain, at least for m > 2. Known estimates for the r ...
... While conditions for convergence of this method are readily established, useful theoretical estimates of the rate of convergence of the Kaczmarz method (or more generally of the alternating projection method for linear subspaces) are difficult to obtain, at least for m > 2. Known estimates for the r ...
1 Numerical Solution to Quadratic Equations 2 Finding Square
... by evaluating the function at the midpoint of the interval. These two methods are depicted in Figure 3. Using these methods, we can calculate the definite integral by simply evaluating the original function at definite points, which we should always be able to do (the prevailing assumption is that w ...
... by evaluating the function at the midpoint of the interval. These two methods are depicted in Figure 3. Using these methods, we can calculate the definite integral by simply evaluating the original function at definite points, which we should always be able to do (the prevailing assumption is that w ...
lecture2-planning-p
... Why does this help? V¼ = r¼ + ° P¼ t °t P¼t r¼ = r¼ + ° P¼ V¼ Also explains why smoothness of the reward function is not required ...
... Why does this help? V¼ = r¼ + ° P¼ t °t P¼t r¼ = r¼ + ° P¼ V¼ Also explains why smoothness of the reward function is not required ...
Numerical Learning
... P (pos) = (9 + 1)/(14 + 2) = 10/16 P (neg) = (5 + 1)/(14 + 2) = 6/16 P (sunny | pos) = (2 + 1)/(9 + 3) = 3/12 P (overcast | pos) = (4 + 1)/(9 + 3) = 5/12 P (rain | pos) = (3 + 1)/(9 + 3) = 4/12 CS 5233 Artificial Intelligence ...
... P (pos) = (9 + 1)/(14 + 2) = 10/16 P (neg) = (5 + 1)/(14 + 2) = 6/16 P (sunny | pos) = (2 + 1)/(9 + 3) = 3/12 P (overcast | pos) = (4 + 1)/(9 + 3) = 5/12 P (rain | pos) = (3 + 1)/(9 + 3) = 4/12 CS 5233 Artificial Intelligence ...
Parallel Processing, Part 1
... uniprocessor, would still take 400 centuries even if it can be perfectly parallelized over 1 billion processors. ...
... uniprocessor, would still take 400 centuries even if it can be perfectly parallelized over 1 billion processors. ...
Final Exam: 15-853Algorithm in the real and virtual world
... If the k component of ek are all “0”s, the equation above reduces to ck = mkGk’ Thus, Mallory can recover the sender’s message without decoding (since c’ and G’ are known). If error vector e is an n-bit vector with t “1”s and n – t “0”s, the probability of choosing (without replacement) k “0”s compo ...
... If the k component of ek are all “0”s, the equation above reduces to ck = mkGk’ Thus, Mallory can recover the sender’s message without decoding (since c’ and G’ are known). If error vector e is an n-bit vector with t “1”s and n – t “0”s, the probability of choosing (without replacement) k “0”s compo ...
Accelerating Correctly Rounded Floating
... In Section 5.1, we show that, under some conditions on y, that could be checked at compile-time, we can return a correctly rounded quotient using one multiplication and one fused-mac. In Section 5.2, we show that, if a larger internal precision than the target precision is available (one more bit su ...
... In Section 5.1, we show that, under some conditions on y, that could be checked at compile-time, we can return a correctly rounded quotient using one multiplication and one fused-mac. In Section 5.2, we show that, if a larger internal precision than the target precision is available (one more bit su ...
Lecture 3 - United International College
... • Given points a and b that bracket a root, find x = ½ (a+ b) and evaluate f(x) • If f(x) and f(b) have the same sign (+ or -) then b x else a x • Stop when a and b are “close enough” • If function is continuous, this will succeed in finding some root. ...
... • Given points a and b that bracket a root, find x = ½ (a+ b) and evaluate f(x) • If f(x) and f(b) have the same sign (+ or -) then b x else a x • Stop when a and b are “close enough” • If function is continuous, this will succeed in finding some root. ...
Chapter 12: Copying with the Limitations of Algorithm Power
... Approximation Scheme for Knapsack Problem Step 1: Order the items in decreasing order of relative values: v1/w1 ⋯ vn/wn Step 2: For a given integer parameter k, 0 ≤ k ≤ n, generate all subsets of k items or less and for each of those that fit the knapsack, add the remaining items in decreasing ...
... Approximation Scheme for Knapsack Problem Step 1: Order the items in decreasing order of relative values: v1/w1 ⋯ vn/wn Step 2: For a given integer parameter k, 0 ≤ k ≤ n, generate all subsets of k items or less and for each of those that fit the knapsack, add the remaining items in decreasing ...
Style E 24 by 48
... “A Noise-Tolerant Fejér-based modified-FBP Reconstruction Algorithm (Fejér-mFBP) for Positron Emission Tomography”, C.E. Beni, O.P. Bruno (to be submitted) ...
... “A Noise-Tolerant Fejér-based modified-FBP Reconstruction Algorithm (Fejér-mFBP) for Positron Emission Tomography”, C.E. Beni, O.P. Bruno (to be submitted) ...
16. Algorithm stability
... • an algorithm is unstable if rounding errors cause large errors in the result • rigorous definition depends on what ‘accurate’ and ‘large error’ mean • instability is often, but not always, caused by cancellation ...
... • an algorithm is unstable if rounding errors cause large errors in the result • rigorous definition depends on what ‘accurate’ and ‘large error’ mean • instability is often, but not always, caused by cancellation ...
A Randomized Approximate Nearest Neighbors
... Given a collection of n points x1 , x2 , . . . , xn in Rd and an integer k << n, the task of finding the k nearest neighbors for each xi is known as the “Nearest Neighbors Problem”; it is ubiquitous in a number of areas of Computer Science: Machine Learning, Data Mining, Artificial Intelligence, etc ...
... Given a collection of n points x1 , x2 , . . . , xn in Rd and an integer k << n, the task of finding the k nearest neighbors for each xi is known as the “Nearest Neighbors Problem”; it is ubiquitous in a number of areas of Computer Science: Machine Learning, Data Mining, Artificial Intelligence, etc ...
Cooley–Tukey FFT algorithm

The Cooley–Tukey algorithm, named after J.W. Cooley and John Tukey, is the most common fast Fourier transform (FFT) algorithm. It re-expresses the discrete Fourier transform (DFT) of an arbitrary composite size N = N1N2 in terms of smaller DFTs of sizes N1 and N2, recursively, to reduce the computation time to O(N log N) for highly composite N (smooth numbers). Because of the algorithm's importance, specific variants and implementation styles have become known by their own names, as described below.Because the Cooley-Tukey algorithm breaks the DFT into smaller DFTs, it can be combined arbitrarily with any other algorithm for the DFT. For example, Rader's or Bluestein's algorithm can be used to handle large prime factors that cannot be decomposed by Cooley–Tukey, or the prime-factor algorithm can be exploited for greater efficiency in separating out relatively prime factors.The algorithm, along with its recursive application, was invented by Carl Friedrich Gauss. Cooley and Tukey independently rediscovered and popularized it 160 years later.