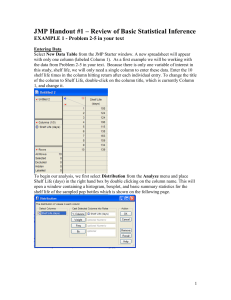
Chi Square
... • The most frequent reason this happens is when data are not interval. • To make inferences, some characteristic of the data must approximate a probability distribution. • These are call non-parametric statistics. ...
... • The most frequent reason this happens is when data are not interval. • To make inferences, some characteristic of the data must approximate a probability distribution. • These are call non-parametric statistics. ...
Measures of Center
... → The mean is pulled by extreme observations or outliers. So it is not a resistant measure of center. → The median is not pulled by the outliers. So it is a resistant measure of center. Q: In figuring Phyllis’ grade, her instructor needs to know total HW points she scored but lost this info. Which w ...
... → The mean is pulled by extreme observations or outliers. So it is not a resistant measure of center. → The median is not pulled by the outliers. So it is a resistant measure of center. Q: In figuring Phyllis’ grade, her instructor needs to know total HW points she scored but lost this info. Which w ...
Lesson Plan: Z-Tables - Howard County Public School System
... peoples’ heights, IQ) and this curve has specific properties. Ask groups to find the percentage of the scores that fall between the Mean one Standard Deviation, the Mean two Standard Deviations, and the Mean three Standard Deviations (answers should be approximately 68%, 95%, and 99.7%). These ...
... peoples’ heights, IQ) and this curve has specific properties. Ask groups to find the percentage of the scores that fall between the Mean one Standard Deviation, the Mean two Standard Deviations, and the Mean three Standard Deviations (answers should be approximately 68%, 95%, and 99.7%). These ...