Dielectric Polarization and Particle Shape Effects
... P. Feynman, “there’s plenty of room at the bottom,” is astonishingly still valid in the era of nanotechnology [2]. But there is another view at the effect of scaling. Not all remain the same when the amplification in our microscope is increased and we are dealing with objects of smaller dimension. A ...
... P. Feynman, “there’s plenty of room at the bottom,” is astonishingly still valid in the era of nanotechnology [2]. But there is another view at the effect of scaling. Not all remain the same when the amplification in our microscope is increased and we are dealing with objects of smaller dimension. A ...
Topics: • Electric Potential of continuous charge distributions
... If the inner shell has a net charge +q, and the outer shell has no net charge, how is the charge distributed? What about electric potential? find the E field everywhere. ...
... If the inner shell has a net charge +q, and the outer shell has no net charge, how is the charge distributed? What about electric potential? find the E field everywhere. ...
Two-point microrheology and the electrostatic analogy
... sphere allow one to calculate, using the response function, Eq. 共1兲, the fluid’s viscosity. This viscosity encodes all the rheology of the Newtonian fluid. We have already examined the validity of the generalization of the GSER to a viscoelastic medium in previous paper 关5,6兴 and have found that in ...
... sphere allow one to calculate, using the response function, Eq. 共1兲, the fluid’s viscosity. This viscosity encodes all the rheology of the Newtonian fluid. We have already examined the validity of the generalization of the GSER to a viscoelastic medium in previous paper 关5,6兴 and have found that in ...
Quasi-static electromagnetic fields created by - E-Journal
... Independently of the dipole orientation, the electric field (inside or outside) arises from a point dipole and a line-current distribution. The electric field created by the point dipole resembles the quasi-static field created for a dipole in the vicinity of a planar interface. For the case of the ...
... Independently of the dipole orientation, the electric field (inside or outside) arises from a point dipole and a line-current distribution. The electric field created by the point dipole resembles the quasi-static field created for a dipole in the vicinity of a planar interface. For the case of the ...
CLASSICAL FIELDS - Instituto de Física Teórica
... of that observer. There is, however, a preferred class of frames, in which all measurements give the same results, the so-called inertial frames. Such frames are characterized by the following property: a particle not subject to any force moves with constant velocity. This is not true if the particl ...
... of that observer. There is, however, a preferred class of frames, in which all measurements give the same results, the so-called inertial frames. Such frames are characterized by the following property: a particle not subject to any force moves with constant velocity. This is not true if the particl ...
Electrostatic analysis of the interactions between charged particles
... The action of charges under their mutual influence is obtained from Gauss’s law that couples uniquely the surface potential with the distribution and magnitude of electrical charge on the surface of the spheres. The effect of the surface charge is integrated to obtain an analytical expression for th ...
... The action of charges under their mutual influence is obtained from Gauss’s law that couples uniquely the surface potential with the distribution and magnitude of electrical charge on the surface of the spheres. The effect of the surface charge is integrated to obtain an analytical expression for th ...
32 From Galileo to Lorentz transformations
... 32.3: Galileo transformations of space-time coordinates and Newtonian mechanics When is an object subject to no force? Experience shows that all known real forces are due to the existence of something which is the source of the force and that the intensity of all real forces decreases when increasin ...
... 32.3: Galileo transformations of space-time coordinates and Newtonian mechanics When is an object subject to no force? Experience shows that all known real forces are due to the existence of something which is the source of the force and that the intensity of all real forces decreases when increasin ...
General Relativity: An Informal Primer 1 Introduction
... coordinate system, such as Ex or Bz . In fact, this is precisely how Maxwell himself manipulated his own equations in the 1850s and 1860s, and a large part of the reason why his famous Treatise on Electricity and Magnetism, published in 1873, filled two hulking volumes and totaled nearly 1000 pages ...
... coordinate system, such as Ex or Bz . In fact, this is precisely how Maxwell himself manipulated his own equations in the 1850s and 1860s, and a large part of the reason why his famous Treatise on Electricity and Magnetism, published in 1873, filled two hulking volumes and totaled nearly 1000 pages ...
Chapter 10: Relativistic Quantum Mechanics
... The replacement of (10.2) by Lorentz–invariant equations will have two surprising and extremely important consequences: some of the equations need to be formulated in a representation for which the wave functions ψ(~r, t) are vectors of dimension larger one, the components representing the spin attr ...
... The replacement of (10.2) by Lorentz–invariant equations will have two surprising and extremely important consequences: some of the equations need to be formulated in a representation for which the wave functions ψ(~r, t) are vectors of dimension larger one, the components representing the spin attr ...
Powerpoint
... frictionless plastic air pucks that ride on an air table as shown below. The pucks are held in place as a charge of 2.0 x 10-8 C is placed on sphere A on the left and a charge of 6.0 x 10-6 C is placed on sphere B on the right. The pucks are then released so that the pucks with the spheres attached ...
... frictionless plastic air pucks that ride on an air table as shown below. The pucks are held in place as a charge of 2.0 x 10-8 C is placed on sphere A on the left and a charge of 6.0 x 10-6 C is placed on sphere B on the right. The pucks are then released so that the pucks with the spheres attached ...
Electromagnetic surface and line sources under coordinate
... distribution radiate like an entirely different one. Conformal antennas are one potential application of such an approach, in which currents may be constrained to a given surface but one wishes to have these currents radiate as if they were in a different location or had a different shape 关7兴. Kundt ...
... distribution radiate like an entirely different one. Conformal antennas are one potential application of such an approach, in which currents may be constrained to a given surface but one wishes to have these currents radiate as if they were in a different location or had a different shape 关7兴. Kundt ...
Abstract:
... variables for these different forces. We also demonstrate with this lab that charge is quantized. Charge is restricted to discrete values, and is not continuous. Charge has the nature that it comes in “chunks.” As expected, each sphere has a different number of “chunks” or electrons. When we observe ...
... variables for these different forces. We also demonstrate with this lab that charge is quantized. Charge is restricted to discrete values, and is not continuous. Charge has the nature that it comes in “chunks.” As expected, each sphere has a different number of “chunks” or electrons. When we observe ...
Supplemental Lecture II: Special Relativity in Tensor Notation
... The 0th component of the four-vector is called the timelike component, and others are called the spacelike components. Notice that we have replaced the Latin index by a Greek index; from now on Greek indices will denote four-vectors while Latin indices will denote three-vectors. Note also that the i ...
... The 0th component of the four-vector is called the timelike component, and others are called the spacelike components. Notice that we have replaced the Latin index by a Greek index; from now on Greek indices will denote four-vectors while Latin indices will denote three-vectors. Note also that the i ...
Introduction to the Maxwell Garnett approximation: tutorial
... Let us now place the whole system in a constant external electric field Eext . We will neglect the electromagnetic interaction of all the dipoles since we have decided to neglect the regular part of the dipole field in (2). Again, the assumption that we use is that this field is unimportant because ...
... Let us now place the whole system in a constant external electric field Eext . We will neglect the electromagnetic interaction of all the dipoles since we have decided to neglect the regular part of the dipole field in (2). Again, the assumption that we use is that this field is unimportant because ...
Relativity without tears - Philsci
... relativity was considered shocking, anti-establishment and highly mysterious, and all presentations intended for the population at large were meant to emphasize these shocking and mysterious aspects, which is hardly conducive to easy teaching and good understanding. They tended to emphasize the revo ...
... relativity was considered shocking, anti-establishment and highly mysterious, and all presentations intended for the population at large were meant to emphasize these shocking and mysterious aspects, which is hardly conducive to easy teaching and good understanding. They tended to emphasize the revo ...
Millikan Oil Drop - University of Colorado Boulder
... The first person to measure accurately the electron’s charge was the American physicist R. A. Millikan. Working at the University of Chicago in 1912, Millikan found that droplets of oil from a simple ...
... The first person to measure accurately the electron’s charge was the American physicist R. A. Millikan. Working at the University of Chicago in 1912, Millikan found that droplets of oil from a simple ...
Chapter 22 – Gauss` Law and Flux
... Surface integral over sphere • Compute the surface integral of E(r) over a sphere of radius r with the charge q at the center. • E(r) dA = 4r2 * kq/r2 = 4kq = q/0 • (NOTE: no r dependence) k=1/40 • E(r0) = 0 – this is true of ANY inverse square field (Gravity also) • E(r=0) = (r) func ...
... Surface integral over sphere • Compute the surface integral of E(r) over a sphere of radius r with the charge q at the center. • E(r) dA = 4r2 * kq/r2 = 4kq = q/0 • (NOTE: no r dependence) k=1/40 • E(r0) = 0 – this is true of ANY inverse square field (Gravity also) • E(r=0) = (r) func ...
Jackson 4.9 Homework Solution
... A point charge q is located in free space a distance d from the center of a dielectric sphere of radius a (a < d) and dielectric constant ε/ε0. (a) Find the potential at all points in space as an expansion in spherical harmonics. (b) Calculate the rectangular components of the electric field near th ...
... A point charge q is located in free space a distance d from the center of a dielectric sphere of radius a (a < d) and dielectric constant ε/ε0. (a) Find the potential at all points in space as an expansion in spherical harmonics. (b) Calculate the rectangular components of the electric field near th ...
Physics 2426 Engineering Physics II Review Problems Exam 1
... 71. A parallel plate capacitor of area A = 30 cm2 and separation d = 5 mm is charged by a battery of 60-V. If the air between the plates is replaced by a dielectric of κ = 4 with the battery still connected, then what is the ratio of the initial charge on the plates divided by the final charge on th ...
... 71. A parallel plate capacitor of area A = 30 cm2 and separation d = 5 mm is charged by a battery of 60-V. If the air between the plates is replaced by a dielectric of κ = 4 with the battery still connected, then what is the ratio of the initial charge on the plates divided by the final charge on th ...
F33OT2 Symmetry and Action and Principles in Physics Contents
... The idea of the least-action principle, which you studied in F33OT1 in the context of Classical Mechanics, originates with Fermat in the 1660s. Fermat’s principle states that the path followed by a ray of light between two points is the one that takes the least time. This variational principle allow ...
... The idea of the least-action principle, which you studied in F33OT1 in the context of Classical Mechanics, originates with Fermat in the 1660s. Fermat’s principle states that the path followed by a ray of light between two points is the one that takes the least time. This variational principle allow ...
Millikan Oil-Drop Experiment
... Electrons were observed around the turn of the century by J.J. Thomson when he measured the ratio of the electron's charge to its mass (e/m). However, Thomson's experiment only gave a value for the ratio e/m. The charge of the electron was measured by Millikan in a now classic experiment performed b ...
... Electrons were observed around the turn of the century by J.J. Thomson when he measured the ratio of the electron's charge to its mass (e/m). However, Thomson's experiment only gave a value for the ratio e/m. The charge of the electron was measured by Millikan in a now classic experiment performed b ...
Lecture 19
... As the cylinders are infinite, the potential or the electric field have no z dependence and the plane, where the cross sections are circles. We can variation is only in the two dimensional , in the do a conformal mapping . Since polar equation to a circle is . We will map this onto the w-plane by a ...
... As the cylinders are infinite, the potential or the electric field have no z dependence and the plane, where the cross sections are circles. We can variation is only in the two dimensional , in the do a conformal mapping . Since polar equation to a circle is . We will map this onto the w-plane by a ...
Classical Field Theory
... example such as a temperature field. Suppose we start with an initial field φ(~x) = T (~x) which has a hotspot at, say, ~x = (1, 0, 0). After a rotation, ~x → R~x about the z-axis, the new field, φ′ (~x) will have the hotspot at, say ~x = (0, 1, 0). We want now to express the new field φ′ (~x) in te ...
... example such as a temperature field. Suppose we start with an initial field φ(~x) = T (~x) which has a hotspot at, say, ~x = (1, 0, 0). After a rotation, ~x → R~x about the z-axis, the new field, φ′ (~x) will have the hotspot at, say ~x = (0, 1, 0). We want now to express the new field φ′ (~x) in te ...
AP B Physics Chapter 18 Electrostatics #2
... number of electrons. If the protons could somehow be separated from the electrons and placed in separate containers separated by 1.00 x 103 m, what would be the magnitude of the electrostatic force exerted by one box on the other? A) ...
... number of electrons. If the protons could somehow be separated from the electrons and placed in separate containers separated by 1.00 x 103 m, what would be the magnitude of the electrostatic force exerted by one box on the other? A) ...
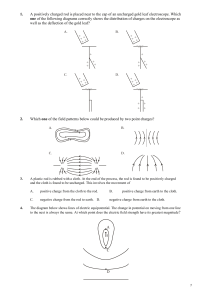
1 - Moodle Ecolint
... The diagram below shows lines of electric equipotential. The change in potential on moving from one line to the next is always the same. At which point does the electric field strength have its greatest magnitude ? ...
... The diagram below shows lines of electric equipotential. The change in potential on moving from one line to the next is always the same. At which point does the electric field strength have its greatest magnitude ? ...