1222grading1198 - Emerson Statistics
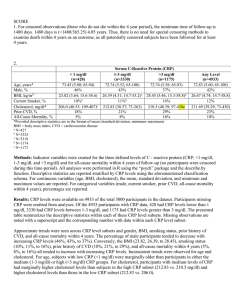
... CRP+1 was used so that participants with CRP=0 would not return an unusable value. A two-sided t-test allowing for the possibility of unequal variances was used to compare the differences in ln(CRP+1) between those who died within 4 years and those who survived. A 95% confidence interval for the dif ...
... CRP+1 was used so that participants with CRP=0 would not return an unusable value. A two-sided t-test allowing for the possibility of unequal variances was used to compare the differences in ln(CRP+1) between those who died within 4 years and those who survived. A 95% confidence interval for the dif ...
theory of errors
... theoryand mathematical statistics is the science which specializes in studies of random (or stochastic) events, variables and functions. It will serve as the theoretical base for our treatment of the random measurement errors. In Chapter 6, we will brie.y discuss how to detect gross errors and syste ...
... theoryand mathematical statistics is the science which specializes in studies of random (or stochastic) events, variables and functions. It will serve as the theoretical base for our treatment of the random measurement errors. In Chapter 6, we will brie.y discuss how to detect gross errors and syste ...
2. MEASUREMENT AND ERROR
... one another i.e., a measure of reproducibility or agreement with each other for multiple trials. Sensitivity: the ability of the measuring instrument to respond to changes in the measured quantity. It is expressed as the ratio of the change of output signal or response of the instrument to a change ...
... one another i.e., a measure of reproducibility or agreement with each other for multiple trials. Sensitivity: the ability of the measuring instrument to respond to changes in the measured quantity. It is expressed as the ratio of the change of output signal or response of the instrument to a change ...
Uncertainty due to Finite Resolution Measurements
... nearly the same result, within one or two units of the least count (i.e. resolution) of the instrument. (In principle the caliper would be more accurate with an additional display digit, however, customers perceive quality as the ability of the instrument to yield the same value for repeated measure ...
... nearly the same result, within one or two units of the least count (i.e. resolution) of the instrument. (In principle the caliper would be more accurate with an additional display digit, however, customers perceive quality as the ability of the instrument to yield the same value for repeated measure ...
Class 5 - Errors in Measurement
... Instrument calibration is a very important consideration in measurement systems as all instruments suffer drift in their characteristics, and the rate at which this happens depends on many factors, including environmental conditions in which instruments are used and the frequency of their use. T ...
... Instrument calibration is a very important consideration in measurement systems as all instruments suffer drift in their characteristics, and the rate at which this happens depends on many factors, including environmental conditions in which instruments are used and the frequency of their use. T ...
Extremal axioms: logical, mathematical and cognitive aspects
... in many specific ways. As a result, one obtains a whole hierarchy of large cardinal numbers. Zermelo has postulated in 1930 the existence of a transfinite hierarchy of strongly inaccessible numbers. Today strongly inaccessible numbers are the smallest of the huge family of large cardinal numbers. La ...
... in many specific ways. As a result, one obtains a whole hierarchy of large cardinal numbers. Zermelo has postulated in 1930 the existence of a transfinite hierarchy of strongly inaccessible numbers. Today strongly inaccessible numbers are the smallest of the huge family of large cardinal numbers. La ...
chapter5 - CP Chemistry
... 1. To learn how dimensional analysis can be used to solve problems 2. To learn the three temperature scales 3. To learn to convert from one temperature scale to another 4. To practice using problem solving techniques 5. To define density and its units ...
... 1. To learn how dimensional analysis can be used to solve problems 2. To learn the three temperature scales 3. To learn to convert from one temperature scale to another 4. To practice using problem solving techniques 5. To define density and its units ...
Measurement of Water Vapor in Sulphur Hexafluoride
... To ensure that corrosive electrolytes remain at low concentration levels, it is important to make periodic measurements of the water vapor content of the gas used within the SF6 filled equipment. Chilled mirror technology is commonly used as an accurate, reliable, and robust method for measurement o ...
... To ensure that corrosive electrolytes remain at low concentration levels, it is important to make periodic measurements of the water vapor content of the gas used within the SF6 filled equipment. Chilled mirror technology is commonly used as an accurate, reliable, and robust method for measurement o ...
Uncertainties - transmille.net
... Measurement All measurements, even the most accurate, have an unknown inaccuracy or doubt. The is known as the UNCERTAINTY As there is always an uncertainty with any measurement we need to estimate this amount. We also need to calculate our confidence in the estimate of uncertainty, which is how sur ...
... Measurement All measurements, even the most accurate, have an unknown inaccuracy or doubt. The is known as the UNCERTAINTY As there is always an uncertainty with any measurement we need to estimate this amount. We also need to calculate our confidence in the estimate of uncertainty, which is how sur ...
1 Precision Estimates - Physics Department, Princeton University
... In the Ph101 laboratory you will have the opportunity to make several measurements, and likely in later years you will have the need to evaluate the merits of measurements made by others. Typically a good understanding of the precision of the measurements is at least as important as the measured val ...
... In the Ph101 laboratory you will have the opportunity to make several measurements, and likely in later years you will have the need to evaluate the merits of measurements made by others. Typically a good understanding of the precision of the measurements is at least as important as the measured val ...
EXPERIMENTAL ERROR “Absolute certainty is a privilege of
... For example, in reading the ruler for measuring the edge of the book, it is best to use a reference other than the edge of the ruler. Thus a reading at one end of the ruler might be 2.0 cm and at the other end 26.9 cm. The length of the edge of the book is the difference of these two measurements or ...
... For example, in reading the ruler for measuring the edge of the book, it is best to use a reference other than the edge of the ruler. Thus a reading at one end of the ruler might be 2.0 cm and at the other end 26.9 cm. The length of the edge of the book is the difference of these two measurements or ...
Solution
... 2. Let R1 and R2 be any two equivalence relations on the same set A. Examine the properties of R1 R2 and determine if it is a relation of equivalence or not. (prove /disprove each property) R1 R2 is not a relation of equivalence because it is not necessarily transitive. Here is an example of two ...
... 2. Let R1 and R2 be any two equivalence relations on the same set A. Examine the properties of R1 R2 and determine if it is a relation of equivalence or not. (prove /disprove each property) R1 R2 is not a relation of equivalence because it is not necessarily transitive. Here is an example of two ...
Sensors Auto-calibration Method - Using Programmable Interface Circuit Front-end
... required measurement accuracy. The existing conventional correction techniques are essentially based either on the hardware adjustment of the sensor response [1], or on lookup tables [2]. The calibration of sensors using these methods is usually of a high cost and time consuming. For different types ...
... required measurement accuracy. The existing conventional correction techniques are essentially based either on the hardware adjustment of the sensor response [1], or on lookup tables [2]. The calibration of sensors using these methods is usually of a high cost and time consuming. For different types ...























