Logistic Regression Models for Ordinal Response Variables
... categories such as mild (1), moderate (2), and severe (3). In Knapp’s research, the numbers ascribed to the severity of illness categories represent increasing severity, in the sense that “moderate” is more critical than “mild,” and “severe” is more critical than “moderate.” The numerical rating giv ...
... categories such as mild (1), moderate (2), and severe (3). In Knapp’s research, the numbers ascribed to the severity of illness categories represent increasing severity, in the sense that “moderate” is more critical than “mild,” and “severe” is more critical than “moderate.” The numerical rating giv ...
A framework for the investigation of pleiotropy in two
... mutually independent, or not in linkage disequilibrium (LD). The veracity of this assumption can be further scrutinised by using external data resources that catalogue LD structure across the genome (see for example http://www.internationalgenome.org/). In many cases, this restriction still allows h ...
... mutually independent, or not in linkage disequilibrium (LD). The veracity of this assumption can be further scrutinised by using external data resources that catalogue LD structure across the genome (see for example http://www.internationalgenome.org/). In many cases, this restriction still allows h ...
The GENMOD Procedure
... where yi is the response variable for the i th observation. The quantity xi is a column vector of covariates, or explanatory variables, for observation i that is known from the experimental setting and is considered to be fixed, or nonrandom. The vector of unknown coefficients ˇ is estimated by a le ...
... where yi is the response variable for the i th observation. The quantity xi is a column vector of covariates, or explanatory variables, for observation i that is known from the experimental setting and is considered to be fixed, or nonrandom. The vector of unknown coefficients ˇ is estimated by a le ...
Chapter 22: Simultaneous Equation Models – Introduction
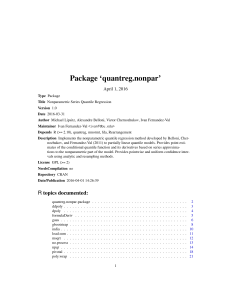
... i. Will the demand curve shift? Explain. ii. Will the supply curve shift? Explain. iii. On a sheet of graph paper, plot the demand curve(s), the supply curve(s), and the two equilibria. iv. Based on the numerical values of the two equilibria can you calculate the slope of the supply curve? Explain. ...
... i. Will the demand curve shift? Explain. ii. Will the supply curve shift? Explain. iii. On a sheet of graph paper, plot the demand curve(s), the supply curve(s), and the two equilibria. iv. Based on the numerical values of the two equilibria can you calculate the slope of the supply curve? Explain. ...
stcurve
... correction near the boundary is performed using boundary kernels. For other kernels, the plotted range of the smoothed hazard function is restricted to be inside of one bandwidth from each endpoint. For these other kernels, specifying noboundary merely removes this range restriction. ...
... correction near the boundary is performed using boundary kernels. For other kernels, the plotted range of the smoothed hazard function is restricted to be inside of one bandwidth from each endpoint. For these other kernels, specifying noboundary merely removes this range restriction. ...
Maximum Likelihood Estimation and the Bayesian Information
... When an obvious estimator exists the method of ML often will find it. The method can be applied to many statistical problems: regression analysis, analysis of variance, discriminant analysis, hypothesis testing, principal components, etc. ...
... When an obvious estimator exists the method of ML often will find it. The method can be applied to many statistical problems: regression analysis, analysis of variance, discriminant analysis, hypothesis testing, principal components, etc. ...
PPT slides for 10 November (Bayes Factors).
... We will talk about a Bayesian ANOVA later, but we can consider the ttest equivalent of these tests: ...
... We will talk about a Bayesian ANOVA later, but we can consider the ttest equivalent of these tests: ...
fuzzy classification models based on tanaka`s fuzzy
... deal with fuzzy uncertainty imbedded in data in different ways. For example, FRC method deals with fuzzy type of uncertainty by modeling the relationship between cluster membership and class membership values. Methods based on fuzzy functions such as FCF and IFCF on the other hand, reflect the fuzzi ...
... deal with fuzzy uncertainty imbedded in data in different ways. For example, FRC method deals with fuzzy type of uncertainty by modeling the relationship between cluster membership and class membership values. Methods based on fuzzy functions such as FCF and IFCF on the other hand, reflect the fuzzi ...
Macroeconomic Factors and the U.S. Stock Market Index: A
... past values of the set of macro-variables possess a certain forecasting ability with respect to U.S. stock prices. By performing an impulse-response analysis, the short-term effect of a shock in each of the macroeconomic factors on the stock market is investigated. The results of this survey highlig ...
... past values of the set of macro-variables possess a certain forecasting ability with respect to U.S. stock prices. By performing an impulse-response analysis, the short-term effect of a shock in each of the macroeconomic factors on the stock market is investigated. The results of this survey highlig ...
Lecture 2: Instrumental Variables
... One could then observe a reduced form which is close to 0 even though treatment e¤ects are positive for everyone (but the compliers are pushed in one direction by the instrument and the de…ers in the other ...
... One could then observe a reduced form which is close to 0 even though treatment e¤ects are positive for everyone (but the compliers are pushed in one direction by the instrument and the de…ers in the other ...
Linear regression
In statistics, linear regression is an approach for modeling the relationship between a scalar dependent variable y and one or more explanatory variables (or independent variables) denoted X. The case of one explanatory variable is called simple linear regression. For more than one explanatory variable, the process is called multiple linear regression. (This term should be distinguished from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable.)In linear regression, data are modeled using linear predictor functions, and unknown model parameters are estimated from the data. Such models are called linear models. Most commonly, linear regression refers to a model in which the conditional mean of y given the value of X is an affine function of X. Less commonly, linear regression could refer to a model in which the median, or some other quantile of the conditional distribution of y given X is expressed as a linear function of X. Like all forms of regression analysis, linear regression focuses on the conditional probability distribution of y given X, rather than on the joint probability distribution of y and X, which is the domain of multivariate analysis.Linear regression was the first type of regression analysis to be studied rigorously, and to be used extensively in practical applications. This is because models which depend linearly on their unknown parameters are easier to fit than models which are non-linearly related to their parameters and because the statistical properties of the resulting estimators are easier to determine.Linear regression has many practical uses. Most applications fall into one of the following two broad categories: If the goal is prediction, or forecasting, or error reduction, linear regression can be used to fit a predictive model to an observed data set of y and X values. After developing such a model, if an additional value of X is then given without its accompanying value of y, the fitted model can be used to make a prediction of the value of y. Given a variable y and a number of variables X1, ..., Xp that may be related to y, linear regression analysis can be applied to quantify the strength of the relationship between y and the Xj, to assess which Xj may have no relationship with y at all, and to identify which subsets of the Xj contain redundant information about y.Linear regression models are often fitted using the least squares approach, but they may also be fitted in other ways, such as by minimizing the ""lack of fit"" in some other norm (as with least absolute deviations regression), or by minimizing a penalized version of the least squares loss function as in ridge regression (L2-norm penalty) and lasso (L1-norm penalty). Conversely, the least squares approach can be used to fit models that are not linear models. Thus, although the terms ""least squares"" and ""linear model"" are closely linked, they are not synonymous.