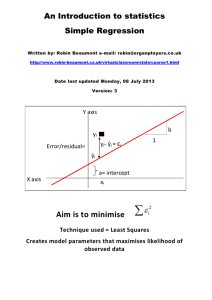
`simple` regression
... ŷi pronounced ‘Y hat’ indicates that it is an estimated value being the value on the line produced by the equation. The i signifies the i’th value, where i takes the value of 1 to n and n is the number of points in the dataset. This variable is the ‘output’ mathematically it is the expectation of ŷi ...
... ŷi pronounced ‘Y hat’ indicates that it is an estimated value being the value on the line produced by the equation. The i signifies the i’th value, where i takes the value of 1 to n and n is the number of points in the dataset. This variable is the ‘output’ mathematically it is the expectation of ŷi ...
Instrumental Variables
... • Military service is endogenous. – Does the military cause a soldier’s future earnings to be a certain amount when he or she leaves the service? Or are there certain characteristics of those that join the military that influence future earnings? » An individual’s choice to enter the service might b ...
... • Military service is endogenous. – Does the military cause a soldier’s future earnings to be a certain amount when he or she leaves the service? Or are there certain characteristics of those that join the military that influence future earnings? » An individual’s choice to enter the service might b ...
Oil Prices and Macro-economy in Russia: The Co
... variables. The null hypothesis is that the number of co-integrating vectors is less than or equal to r against the alternative hypothesis of r > 0. Prior to performing the co-integration tests, we need to estimate the VAR model in levels in order to determine the optimal lag length. Then it was fo ...
... variables. The null hypothesis is that the number of co-integrating vectors is less than or equal to r against the alternative hypothesis of r > 0. Prior to performing the co-integration tests, we need to estimate the VAR model in levels in order to determine the optimal lag length. Then it was fo ...
![Forecasting Methods % M^todos de Previs]o Week 4](http://s1.studyres.com/store/data/015659674_1-198233e0934901d5ec235bc5d18cee7a-300x300.png)
Forecasting Methods % M^todos de Previs]o Week 4
... Actual, Fitted, Residual. These views display the actual and …tted values of the dependent variable and the residuals from the regression in tabular and graphical form. Residual Graph plots only the residuals, while the Standardized Residual Graph plots the residuals divided by the estimated residua ...
... Actual, Fitted, Residual. These views display the actual and …tted values of the dependent variable and the residuals from the regression in tabular and graphical form. Residual Graph plots only the residuals, while the Standardized Residual Graph plots the residuals divided by the estimated residua ...
Heteroskedasticity and Serial Correlation - SelectedWorks
... 1) Is this a multiplicative model? Yes. The model is: yi = βxi + εi . Let ui ∼ iid(0, σ 2 ). Then V ar(yi ) = V ar(εi ) = σ 2 xi 2 implies that εi = xi ui because V ar(xi ui ) = σ 2 x2i . 2) How could you test for heteroskedasticity in this model? ...
... 1) Is this a multiplicative model? Yes. The model is: yi = βxi + εi . Let ui ∼ iid(0, σ 2 ). Then V ar(yi ) = V ar(εi ) = σ 2 xi 2 implies that εi = xi ui because V ar(xi ui ) = σ 2 x2i . 2) How could you test for heteroskedasticity in this model? ...
open ppt file
... A visual inspection of the plot of a data set might indicate that a parabola would be a better model of the data than a straight line. In that case, rather than using linear regression to fit a linear model to the data, we would use quadratic regression on a graphing calculator to find the function ...
... A visual inspection of the plot of a data set might indicate that a parabola would be a better model of the data than a straight line. In that case, rather than using linear regression to fit a linear model to the data, we would use quadratic regression on a graphing calculator to find the function ...
open pdf file
... x values at which the function is undefined represent vertical asymptotes to the graph of the function. A vertical asymptote is a line of the form x = k which the graph of the function approaches but does not cross. In the figure below, which is the graph of the line x = 2 is a ...
... x values at which the function is undefined represent vertical asymptotes to the graph of the function. A vertical asymptote is a line of the form x = k which the graph of the function approaches but does not cross. In the figure below, which is the graph of the line x = 2 is a ...
A Musical Expression Model Using Tonal Tension Tetsuya
... Musical expressionis made by repetition of relaxation and tension. The tension in a score is made from its chord progression, melodic motion and progression, beat structure, rhythmic structure, etc., which depends on not only the structure of the score of music but also the historical interpretation ...
... Musical expressionis made by repetition of relaxation and tension. The tension in a score is made from its chord progression, melodic motion and progression, beat structure, rhythmic structure, etc., which depends on not only the structure of the score of music but also the historical interpretation ...
REFERENCES
... Stewart, G.W. (1993) “On the early history of the singular value decomposition”, SIAM Review, 35: 551-566. Strang, G. (1993) “The fundamental theorem of linear algebra”, The American Mathematical Monthly, 100: 848-855. Strang, G. (2009) Introduction to Linear Algebra, 4th Ed., Wellesley-Cambridge Pr ...
... Stewart, G.W. (1993) “On the early history of the singular value decomposition”, SIAM Review, 35: 551-566. Strang, G. (1993) “The fundamental theorem of linear algebra”, The American Mathematical Monthly, 100: 848-855. Strang, G. (2009) Introduction to Linear Algebra, 4th Ed., Wellesley-Cambridge Pr ...
Document
... • Lazy learners delay modeling the training data until it is needed to classify the test examples. – An example of a lazy leaner is a rote classifier, which memorizes the entire training data and performs classification only if a test instance matches one of the training examples exactly. ...
... • Lazy learners delay modeling the training data until it is needed to classify the test examples. – An example of a lazy leaner is a rote classifier, which memorizes the entire training data and performs classification only if a test instance matches one of the training examples exactly. ...
![AP-Test-Prep---Flashcards[2]](http://s1.studyres.com/store/data/023264297_1-3b04ac15176c964f2860805ab458892d-300x300.png)
AP-Test-Prep---Flashcards[2]
... 1. If the population distribution is normal the sampling distribution will also be normal with the same mean as the population. Additionally, as n increases the sampling distribution’s standard deviation will decrease 2. If the population distribution is not normal the sampling distribution will bec ...
... 1. If the population distribution is normal the sampling distribution will also be normal with the same mean as the population. Additionally, as n increases the sampling distribution’s standard deviation will decrease 2. If the population distribution is not normal the sampling distribution will bec ...
Linear regression
In statistics, linear regression is an approach for modeling the relationship between a scalar dependent variable y and one or more explanatory variables (or independent variables) denoted X. The case of one explanatory variable is called simple linear regression. For more than one explanatory variable, the process is called multiple linear regression. (This term should be distinguished from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable.)In linear regression, data are modeled using linear predictor functions, and unknown model parameters are estimated from the data. Such models are called linear models. Most commonly, linear regression refers to a model in which the conditional mean of y given the value of X is an affine function of X. Less commonly, linear regression could refer to a model in which the median, or some other quantile of the conditional distribution of y given X is expressed as a linear function of X. Like all forms of regression analysis, linear regression focuses on the conditional probability distribution of y given X, rather than on the joint probability distribution of y and X, which is the domain of multivariate analysis.Linear regression was the first type of regression analysis to be studied rigorously, and to be used extensively in practical applications. This is because models which depend linearly on their unknown parameters are easier to fit than models which are non-linearly related to their parameters and because the statistical properties of the resulting estimators are easier to determine.Linear regression has many practical uses. Most applications fall into one of the following two broad categories: If the goal is prediction, or forecasting, or error reduction, linear regression can be used to fit a predictive model to an observed data set of y and X values. After developing such a model, if an additional value of X is then given without its accompanying value of y, the fitted model can be used to make a prediction of the value of y. Given a variable y and a number of variables X1, ..., Xp that may be related to y, linear regression analysis can be applied to quantify the strength of the relationship between y and the Xj, to assess which Xj may have no relationship with y at all, and to identify which subsets of the Xj contain redundant information about y.Linear regression models are often fitted using the least squares approach, but they may also be fitted in other ways, such as by minimizing the ""lack of fit"" in some other norm (as with least absolute deviations regression), or by minimizing a penalized version of the least squares loss function as in ridge regression (L2-norm penalty) and lasso (L1-norm penalty). Conversely, the least squares approach can be used to fit models that are not linear models. Thus, although the terms ""least squares"" and ""linear model"" are closely linked, they are not synonymous.