Regression Analysis
... Abstraction/simplification of the system used as a proxy for the system itself Can try wide-ranging ideas in the model Make your mistakes on the computer where they don’t count, rather for real where they do count Issue of model validity Two types of models ...
... Abstraction/simplification of the system used as a proxy for the system itself Can try wide-ranging ideas in the model Make your mistakes on the computer where they don’t count, rather for real where they do count Issue of model validity Two types of models ...
Spherical Hamiltonian Monte Carlo for Constrained Target Distributions
... HMC improves upon random walk Metropolis by proposing states that are distant from the current state, but nevertheless accepted with high probability. These distant proposals are found by numerically simulating Hamilton dynamics, whose state space consists of its position, denoted by the vector θ, a ...
... HMC improves upon random walk Metropolis by proposing states that are distant from the current state, but nevertheless accepted with high probability. These distant proposals are found by numerically simulating Hamilton dynamics, whose state space consists of its position, denoted by the vector θ, a ...
Nonconcave Penalized Likelihood With NP
... (2001) study the oracle properties of nonconcave penalized likelihood estimators in the finite-dimensional setting. Their results were extended later by Fan and Peng (2004) to the setting of or in a general likelihood framework. be, compared with How large can the dimensionality the sample size , su ...
... (2001) study the oracle properties of nonconcave penalized likelihood estimators in the finite-dimensional setting. Their results were extended later by Fan and Peng (2004) to the setting of or in a general likelihood framework. be, compared with How large can the dimensionality the sample size , su ...
Sure Independence Screening for Ultra
... is an n-vector of i.i.d. random errors. When dimension p is high, it is often assumed that only a small number of predictors among X1 , · · · , Xp contribute to the response, which amounts to assuming ideally that the parameter vector β is sparse. With sparsity, variable selection can improve estima ...
... is an n-vector of i.i.d. random errors. When dimension p is high, it is often assumed that only a small number of predictors among X1 , · · · , Xp contribute to the response, which amounts to assuming ideally that the parameter vector β is sparse. With sparsity, variable selection can improve estima ...
Sure Independence Screening for Ultra
... is an n-vector of i.i.d. random errors. When dimension p is high, it is often assumed that only a small number of predictors among X1 , · · · , Xp contribute to the response, which amounts to assuming ideally that the parameter vector β is sparse. With sparsity, variable selection can improve estima ...
... is an n-vector of i.i.d. random errors. When dimension p is high, it is often assumed that only a small number of predictors among X1 , · · · , Xp contribute to the response, which amounts to assuming ideally that the parameter vector β is sparse. With sparsity, variable selection can improve estima ...
Prediction of continuous phenotypes in mouse, fly, and rice genome
... vector regression default value. Upto the top 900 ranked SNPs both methods give similar correlation coefficients but with all SNPs in the model the ridge regression attains a much higher ...
... vector regression default value. Upto the top 900 ranked SNPs both methods give similar correlation coefficients but with all SNPs in the model the ridge regression attains a much higher ...
here
... Interactive Effects - Ashley Investment Services Issue: The director of personnel is trying to determine whether there are interactive effects in the relationship between employee burnout and time spent socializing with co-workers. ...
... Interactive Effects - Ashley Investment Services Issue: The director of personnel is trying to determine whether there are interactive effects in the relationship between employee burnout and time spent socializing with co-workers. ...
Lab Instructions - University of Alberta Statistics Center
... Adjusted R Square value is an estimate of how well your model would fit another data set from the same population. The value of adjusted R2 is always less than or equal to the value of R2 ; since the estimated regression coefficients are based on the values in this particular data set, the model fit ...
... Adjusted R Square value is an estimate of how well your model would fit another data set from the same population. The value of adjusted R2 is always less than or equal to the value of R2 ; since the estimated regression coefficients are based on the values in this particular data set, the model fit ...
Simple Regression
... way of generating predictions which depend only on the data in an objective fashion. You can say, “Gosh, Boss. I’d really like to hire your kid, but the formula won’t allow it.” 3. Regression Extras. A byproduct of the analysis allows us to determine the accuracy of our predictions. That is, beside ...
... way of generating predictions which depend only on the data in an objective fashion. You can say, “Gosh, Boss. I’d really like to hire your kid, but the formula won’t allow it.” 3. Regression Extras. A byproduct of the analysis allows us to determine the accuracy of our predictions. That is, beside ...
PDF
... SHAZAM version 6.0 econometrics package (White et al.). As summarized in Table 1, all estimates of the coefficient on YEAR lay within one standard error of the estimates from OLS estimates. Coefficient estimates with RR were insignificantly different from OLS despite (1) a disproportionate number of ...
... SHAZAM version 6.0 econometrics package (White et al.). As summarized in Table 1, all estimates of the coefficient on YEAR lay within one standard error of the estimates from OLS estimates. Coefficient estimates with RR were insignificantly different from OLS despite (1) a disproportionate number of ...
PPT Lecture Notes
... the “Dependent” box, and the predictor (i.e., the X-axis variable) in the “Independent(s)” box. • Click the “Statistics” box, and check “estimates”, “model fit”, and “descriptives”. ...
... the “Dependent” box, and the predictor (i.e., the X-axis variable) in the “Independent(s)” box. • Click the “Statistics” box, and check “estimates”, “model fit”, and “descriptives”. ...
Tuesday, June 28: Introduction
... clearly nonlinear for gini • As with the simple model, we could test for nonlinearity using an Ftest, comparing the RSS of this model with the RSS of the linear model • If we had only one more predictor, the lowess model would be impossible to interpret— we can’t see in more than 3 dimensions ...
... clearly nonlinear for gini • As with the simple model, we could test for nonlinearity using an Ftest, comparing the RSS of this model with the RSS of the linear model • If we had only one more predictor, the lowess model would be impossible to interpret— we can’t see in more than 3 dimensions ...
Powerpoint Slides for Unit 10
... • We’ve been doing hypothesis tests for single coefficients • H0: = 0 reject if |t| > t/2,n-k-1 • HA: 0 • What about testing more than one coefficient at the same time? • e.g., want to see if an entire group of 10 dummy variables for 10 industries should be in the model • Joint tests can be c ...
... • We’ve been doing hypothesis tests for single coefficients • H0: = 0 reject if |t| > t/2,n-k-1 • HA: 0 • What about testing more than one coefficient at the same time? • e.g., want to see if an entire group of 10 dummy variables for 10 industries should be in the model • Joint tests can be c ...
Forecasting with Regression Analysis Causal, Explanatory
... • Why is not more variation explained? • Multicollinearity Total variation exists: – X1 is correlated Explained with X2 by X1 – We want independence of Explained by X2 the X’s (uncorrelated) ...
... • Why is not more variation explained? • Multicollinearity Total variation exists: – X1 is correlated Explained with X2 by X1 – We want independence of Explained by X2 the X’s (uncorrelated) ...
Mod18-A Applications of Regression to Water Quality Analysis
... calibrate a lab instrument to predict some response variable – a “calibration curve” In this example, absorbance from a spectrophotometer is measured from series of standards with fixed N concentrations. Once the relationship between absorbance and concentration is established, measuring the abs ...
... calibrate a lab instrument to predict some response variable – a “calibration curve” In this example, absorbance from a spectrophotometer is measured from series of standards with fixed N concentrations. Once the relationship between absorbance and concentration is established, measuring the abs ...
Lecture 9 - Department of Mathematics and Statistics
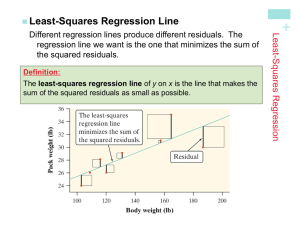
... properties of least-squares regression. They are not true for other methods of fitting a line to data. ...
... properties of least-squares regression. They are not true for other methods of fitting a line to data. ...
PowerPoint Slides 1
... • β2 measures the “direct” or the “net” effect of a unit change in X2 on the mean value of Y, net of any effect that X3 may have on mean Y. • β3 measures the “direct” or “net” effect of a unit change in X3 on the mean value of Y, net of any effect that X2 may have on mean Y. • How do we actually go ...
... • β2 measures the “direct” or the “net” effect of a unit change in X2 on the mean value of Y, net of any effect that X3 may have on mean Y. • β3 measures the “direct” or “net” effect of a unit change in X3 on the mean value of Y, net of any effect that X2 may have on mean Y. • How do we actually go ...
Political Science 30: Political Inquiry
... 57.701% of the time . Since senator #1 “actually” supported the poor on 54% of their tax votes, the prediction error (“e” or “residual”) for senator #1 is: 54 - 57.701 = -3.701 The computer then squares this value (i.e., -3.701 x -3.701 = 13.69). The computer performs this same operation for all 100 ...
... 57.701% of the time . Since senator #1 “actually” supported the poor on 54% of their tax votes, the prediction error (“e” or “residual”) for senator #1 is: 54 - 57.701 = -3.701 The computer then squares this value (i.e., -3.701 x -3.701 = 13.69). The computer performs this same operation for all 100 ...
Linear Regression - Lyle School of Engineering
... Assume data fits a predefined function Determine best values for regression coefficients c0,c1,…,cn. Assume an error: y = c0+c1x1+…+cnxn+e Estimate error using mean squared error for training set: ...
... Assume data fits a predefined function Determine best values for regression coefficients c0,c1,…,cn. Assume an error: y = c0+c1x1+…+cnxn+e Estimate error using mean squared error for training set: ...
Preparing Data for Analysis - Walden University Writing Center
... There are several observations that have a centered leverage value larger than this. It would be important to investigate those observations for accuracy and validity. Observations that have Cook’s distance greater than 4/n can be described as ...
... There are several observations that have a centered leverage value larger than this. It would be important to investigate those observations for accuracy and validity. Observations that have Cook’s distance greater than 4/n can be described as ...
Least-Squares Regression Line
... The number of miles (in thousands) for the 11 used Hondas have a mean of 50.5 and a standard deviation of 19.3. The asking prices had a mean of $14,425 and a standard deviation of $1,899. The correlation for these variables is r = -0.874. Find the equation of the least-squares regression line and ...
... The number of miles (in thousands) for the 11 used Hondas have a mean of 50.5 and a standard deviation of 19.3. The asking prices had a mean of $14,425 and a standard deviation of $1,899. The correlation for these variables is r = -0.874. Find the equation of the least-squares regression line and ...
Lecture 8
... Application Examples of Oja’s Rule Finds the direction (line) which minimizes the sum of the total squared distance from each point to its orthogonal projection onto the line. ...
... Application Examples of Oja’s Rule Finds the direction (line) which minimizes the sum of the total squared distance from each point to its orthogonal projection onto the line. ...
Pivotal Estimation in High-dimensional Regression via
... conic programming. Gautier and Tsybakov (2011) also present a method to obtain finite sample confidence sets that are robust to non-Gaussian and heteroscedastic errors. Another important issue is to relax the assumptions on the model under which the validity of the Lasso type methods is proved, such ...
... conic programming. Gautier and Tsybakov (2011) also present a method to obtain finite sample confidence sets that are robust to non-Gaussian and heteroscedastic errors. Another important issue is to relax the assumptions on the model under which the validity of the Lasso type methods is proved, such ...
Yi(1)
... outcomes known not to be affected by the treatment. Such variables includes covariates that are by definition not affected by the treatment. Such tests are familiar from settings with identification based on unconfoundedness assumptions. Although not required for the validity of the design, in most ...
... outcomes known not to be affected by the treatment. Such variables includes covariates that are by definition not affected by the treatment. Such tests are familiar from settings with identification based on unconfoundedness assumptions. Although not required for the validity of the design, in most ...