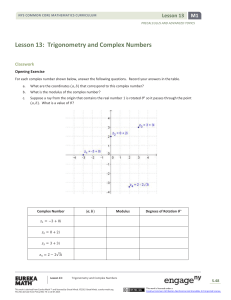
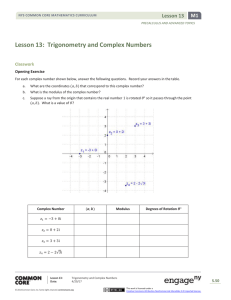
Complex Numbers
... We know that cos θ + ı̇ sin θ is on the circle |z| = 1, and taking powers of it just rotates it around. The only real numbers it could possibly hit are −1 and 1. So we could try to solve (cos θ + ı̇ sin θ)75 = 1 and (cos θ + ı̇ sin θ)75 = −1 separately. But we can also combine these two into (cos θ ...
... We know that cos θ + ı̇ sin θ is on the circle |z| = 1, and taking powers of it just rotates it around. The only real numbers it could possibly hit are −1 and 1. So we could try to solve (cos θ + ı̇ sin θ)75 = 1 and (cos θ + ı̇ sin θ)75 = −1 separately. But we can also combine these two into (cos θ ...
Calibration of Electrical Fast Transient/ Burst Generators
... The real and imaginary axes extend to plus and minus infinity while the magnitude is always non-negative. The phase is cyclical in nature. To avoid these problems, the output quantities of the measurement model should be in terms of real and imaginary parts. Results should only be converted into ...
... The real and imaginary axes extend to plus and minus infinity while the magnitude is always non-negative. The phase is cyclical in nature. To avoid these problems, the output quantities of the measurement model should be in terms of real and imaginary parts. Results should only be converted into ...
Lecture Note 08 EECS 4101/5101 Instructor: Andy Mirzaian All
... -2problem is now to compute, for each vertex pi in this graph, its nearest adjacent vertex p j . But since the graph is complete, it has Θ(n2) edges. The sparsification method will eliminate many irrelevant edges to obtain a sparse subgraph that still contains the edges we are seeking. The sparse g ...
... -2problem is now to compute, for each vertex pi in this graph, its nearest adjacent vertex p j . But since the graph is complete, it has Θ(n2) edges. The sparsification method will eliminate many irrelevant edges to obtain a sparse subgraph that still contains the edges we are seeking. The sparse g ...
Development of Algebra:Cardaro, Tartaglia and Ferrari in 1300`s in
... .44989 -.31462; .44989 -.3146; .449892 -.31462,etc. Euler’s best mathematicin 1700’s like Mozart w/symphonies, travel a lot. Gauss less famous.Newton just respect. Enter=>no money PP fascinated by polynominals. Gauss at the end of the 1700’s (Math student in Germany)became interested in proving tghe ...
... .44989 -.31462; .44989 -.3146; .449892 -.31462,etc. Euler’s best mathematicin 1700’s like Mozart w/symphonies, travel a lot. Gauss less famous.Newton just respect. Enter=>no money PP fascinated by polynominals. Gauss at the end of the 1700’s (Math student in Germany)became interested in proving tghe ...
on the number of sums and products - UBC Math
... Corollary 2 (Szemerédi and Trotter [12]). Given a set of n points on the real plane, the number of k-rich lines (that is, lines incident to at least k points) is O(n2 /k 3 + n/k). In the proof of Theorem 1 we use Theorem 2 and Corollary 2 on Cartesian products only; similar statements are easy to p ...
... Corollary 2 (Szemerédi and Trotter [12]). Given a set of n points on the real plane, the number of k-rich lines (that is, lines incident to at least k points) is O(n2 /k 3 + n/k). In the proof of Theorem 1 we use Theorem 2 and Corollary 2 on Cartesian products only; similar statements are easy to p ...
Answers - updated with answers to tangent planes
... if the above limit exits. Proposition 1. Suppose f : Dn ⊆ Rn → R is differentiable at a point a in Dn . Then − k∇f (a)k 6 ∇f (a) · v 6 k∇f (a)k The maximum of ∇f (a) · v is attained if and only if v = c∇f (a) for some positive number c. The minimum of ∇f (a) · v is attained if and only if v = c∇f (a ...
... if the above limit exits. Proposition 1. Suppose f : Dn ⊆ Rn → R is differentiable at a point a in Dn . Then − k∇f (a)k 6 ∇f (a) · v 6 k∇f (a)k The maximum of ∇f (a) · v is attained if and only if v = c∇f (a) for some positive number c. The minimum of ∇f (a) · v is attained if and only if v = c∇f (a ...
A Graphic Method Of Measuring Vertical Angles From
... skeleton form; 0 is the perspective center, n the nadir point, P the principal point, nha' the picture plane, noh the principal plane, oha' the horizon plane, and noa' a vertical plane through the plumb line on and a picture point a, to which the vertical angle a is to be measured. In Figure 2, the ...
... skeleton form; 0 is the perspective center, n the nadir point, P the principal point, nha' the picture plane, noh the principal plane, oha' the horizon plane, and noa' a vertical plane through the plumb line on and a picture point a, to which the vertical angle a is to be measured. In Figure 2, the ...
Complex Numbers and Phasors
... Modern Version of Steinmetz’ Analysis 1. Begin with a time-dependent analysis problem posed in terms of real variables. 2. Replace the real variables with variables written in terms of complex exponentials; is an eigenfunction of linear ...
... Modern Version of Steinmetz’ Analysis 1. Begin with a time-dependent analysis problem posed in terms of real variables. 2. Replace the real variables with variables written in terms of complex exponentials; is an eigenfunction of linear ...
1.6 Perform Operations with Complex Numbers
... What is a complex conjugate? When do you use it? How do you find the absolute value of a complex number? ...
... What is a complex conjugate? When do you use it? How do you find the absolute value of a complex number? ...
Geometry Name Chapter 3 CENTRAL problem Due Date Core
... For this CENTRAL problem create a slide show using either power point or google slides. You must submit one slide show in google classroom that includes ALL pieces of the CENTRAL problem. Include a title page with name and class hour. ...
... For this CENTRAL problem create a slide show using either power point or google slides. You must submit one slide show in google classroom that includes ALL pieces of the CENTRAL problem. Include a title page with name and class hour. ...
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis. It can be thought of as a modified Cartesian plane, with the real part of a complex number represented by a displacement along the x-axis, and the imaginary part by a displacement along the y-axis.The concept of the complex plane allows a geometric interpretation of complex numbers. Under addition, they add like vectors. The multiplication of two complex numbers can be expressed most easily in polar coordinates—the magnitude or modulus of the product is the product of the two absolute values, or moduli, and the angle or argument of the product is the sum of the two angles, or arguments. In particular, multiplication by a complex number of modulus 1 acts as a rotation.The complex plane is sometimes called the Argand plane because it is used in Argand diagrams. These are named after Jean-Robert Argand (1768–1822), although they were first described by Danish land surveyor and mathematician Caspar Wessel (1745–1818). Argand diagrams are frequently used to plot the positions of the poles and zeroes of a function in the complex plane.